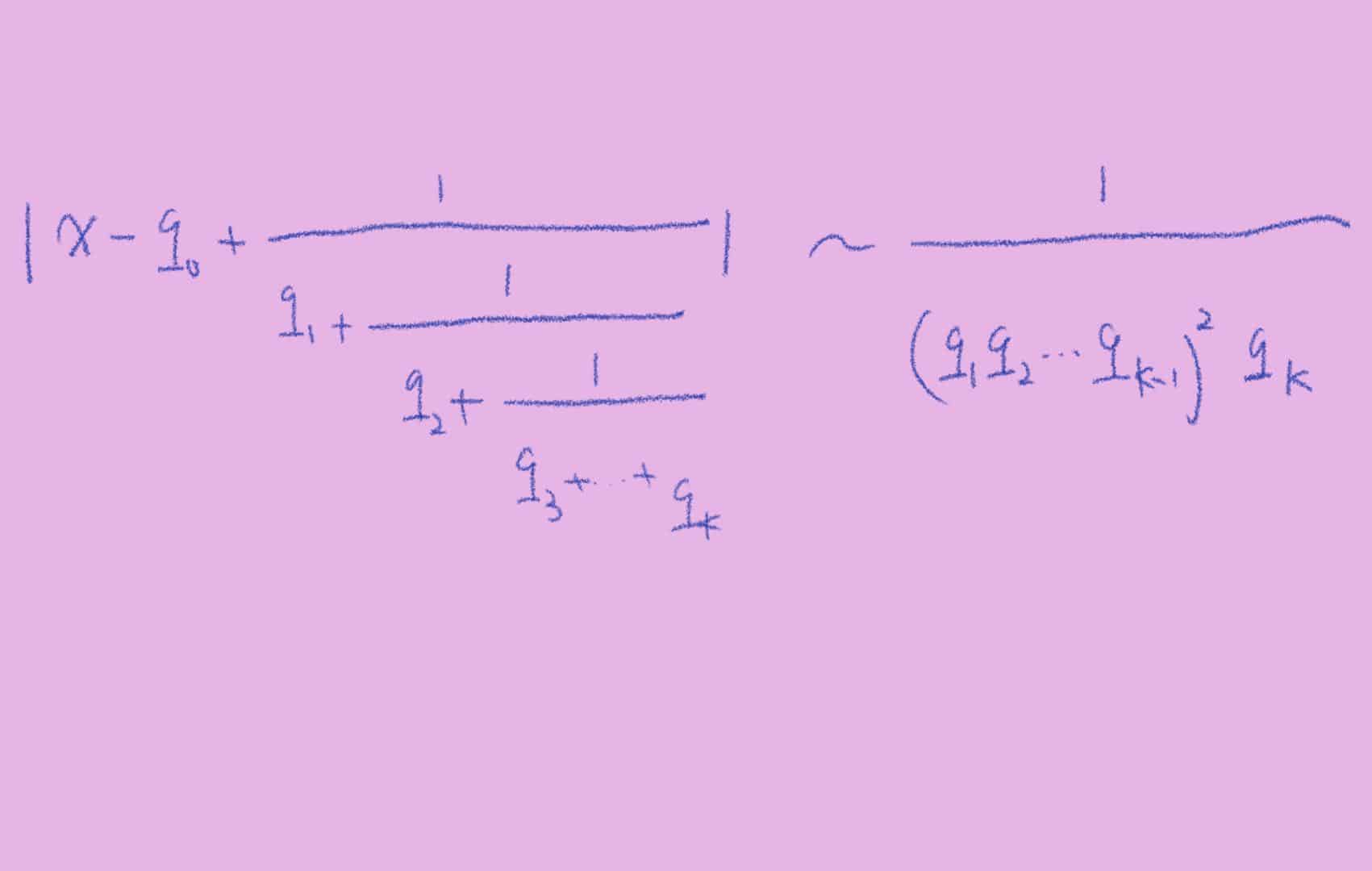I explain some general ideal in the theory of diophantine approximation, some of them is original by myself, begin with a toy model, then consider the application on folklore Swirsing-Schmidt conjecture.
目录
Contents
1. Dirichlet theorem, the toy model
The very basic theorem in the theory of Diophantine approximation is the well known Dirichlet approximation theorem, the statement is following.
Theorem 1 (Dirichlet theorem) for all ${\alpha}$ is a irrational number, we have infinity rational number ${\frac{q}{p}}$ such that:
$\displaystyle |\alpha-\frac{q}{p}|<\frac{1}{p^2} \ \ \ \ \ (1)$
Remark 1 It is easy to see the condition of irrational is crucial. There is a best constant version of it, said, instead of ${1}$, the best constant in the suitable sense for the theorem 1 should be ${\frac{1}{\sqrt{5}}}$ and arrive by ${\frac{\sqrt{5}+1}{2}}$ at least. The strategy of the proof of the best constant version involve the Frey sequences.
Now we begin to explain the strategies to attack the problem.
\paragraph{Argument 1, boxes principle} We begin with a easiest one, i.e. by the argument of box principle, the box principle is following,
Theorem 2 (Boxes principle) Given ${n\in {\mathbb N}}$ and two finite sets ${A={a_1,a_2,…,a_n,a_{n+1}}}$, set ${B={b_1,…,b_{n}}}$, if we have a map:
$\displaystyle f:A\longrightarrow B \ \ \ \ \ (2)$
Then there exists a element ${b_k\in B}$ such that there exist at least two element ${a_i,a_j\in A}$, ${f(a_i)=f(a_j)=b_k}$.
Proof: The proof is trivial. $\Box$
Now consider, ${\forall N\in {\mathbb N}}$, the sequences ${x,2x,…,Nx}$, then ${\{ix\}\in [0,1], \forall i\in \{1,2,…,n\}}$. Divide ${[0,1]}$ in an average way to ${N}$ part: ${[\frac{k-1}{N},\frac{k}{N}]}$. Then the linear structure involve (which, in fact play a crucial role in the approach). And the key point is to look at ${\{nx\}}$ and integers.
\paragraph{Argument 2, continue fractional} We know, for irrational number ${x}$, ${x}$ have a infinite long continue fractional:
$\displaystyle x=q_0+\frac{1}{q_1+\frac{1}{q_2+\frac{1}{q_3+….+\frac{1}{q_k+…}}}} \ \ \ \ \ (3)$
$\displaystyle |x-q_0+\frac{1}{q_1+\frac{1}{q_2+\frac{1}{q_3+….+\frac{1}{q_k}}}}|\sim \frac{1}{(q_1q_2…q_{k-1})^2q_k} \ \ \ \ \ (4)$
And we have,
$\displaystyle \frac{1}{q_1+\frac{1}{q_2+\frac{1}{q_3+….+\frac{1}{q_k}}}}=\frac{a_n}{b_n}, (a_n,b_n)=1 \ \ \ \ \ (5)$
Then ${b_n=O(q_1…q_k)}$.
\paragraph{Argument 3, Bohr set argument} We begin with some kind of Bohr set:
$\displaystyle B_p=I-\cup_{q\in \{0,1,…,p-1\}}(\frac{q}{p}-\frac{1}{p^2},\frac{q}{p}+\frac{1}{p^2}) \ \ \ \ \ (6)$
The key point is the shift of Bohr set, on the vertical line i.e. ${|B_p\cap B_{p+1}|}$ is very slow, and can be explained by
$\displaystyle \frac{k}{p+1}+\frac{1}{(p+1)^2}>\frac{k}{p}-\frac{1}{p^2} \ \ \ \ \ (7)$
So:
$\displaystyle \frac{1}{p^2}+\frac{1}{(p+1)^2}>\frac{k}{p(p+1)} \ \ \ \ \ (8)$
in ${|B_p \cap B_{p+1}|\sim \frac{1}{p(p+1)}}$ But in fact they are not really independent, as the number of Bohr sets increase, then you can calculate the correlation, thanks to the harmonic sires increasing very slowly, wwe can get something non trivial by this argument, but it seems not enough to cover the whole theorem 1.
\paragraph{Argument 4, mountain bootstrap argument} This argument is more clever than 3, although both two arguments try to gain the property we want in 1 from investigate the whole space ${[0,1]}$ but not ${x}$, this argument is more clever.
Now I explain the main argument, it is nothing but sphere packing, with the set of balls
$\displaystyle \Omega=\{B_{p,q}:=(\frac{q}{p}-\frac{1}{q^2},\frac{q}{p}+\frac{1}{p^2})| \forall p\in {\mathbb N}, 1\leq q\leq p-1 \} \ \ \ \ \ (9)$
and define its subset
$\displaystyle \Omega_l=\{B_{p,q}:=(\frac{q}{p}-\frac{1}{q^2},\frac{q}{p}+\frac{1}{p^2})| \forall 1\leq p\leq l, 1\leq q\leq p-1 \} \ \ \ \ \ (10)$
Then ${\Omega_l\subset \Omega}$, and ${\Omega =\cup_{l\in {\mathbb N}}\Omega_l}$. If we can proof,
Lemma 3 For all ${l\in {\mathbb N}}$, there is a subset ${A_l}$ of ${\Omega-\Omega_l}$ such that ${\cup_{i\in A_l}B_i=[0,1]}$.
Remark 2 If we can proof 3, it is easy to see the theorem 1 follows.
Proof: The proof follows very standard in analysis, may be complex analysis? Key point is we start with a ball ${B_{p,q}}$, whatever it is, this is not important, the important thing is we can take some ball ${B_{p’,q’}}$ with the center of ${B_{p’,q’}}$ in ${B_{p,q}}$, then try to consider ${B_{p’,q’}\cup B_{p,q}}$ to extension ${B_{p,q}}$ and then we find the boudary is also larger then we can extension again, step by step just like mountain bootstrap argument. So we involve in two possible ending,
- The extension process could extension ${B{p,q}}$ to whole space.
- we can not use the extension argument to extension to the whole space.
If we are in the first situation, then we are safe, there is nothing need proof. If we are in second case, anyway we take a ball ${B_{p,q}=(\frac{q}{p}-\frac{1}{p^2},\frac{q}{p}+\frac{1}{p^2})}$. Then try to find good ball ${B_{p’,q’}}$ to approximate ${B_{p,q}}$, but this is difficult… $\Box$
Remark 3 Argument 1 is too clever to be true in generalization, argument 2 is standard, by the power of renormalization. argument 3 and argument 4 have gap… I remember I have got a proof similar to argument 4 here many years ago, but I forgot how to get it…
2. Schimidt conjecture
The Schimidt conjecture could be look as the generalization of Dirchlet approximation theorem 1 to algebraic number version, to do this, we need define the height of a algebraic number.
Definition 4 We say a number ${\alpha\in {\mathbb C}}$ is a ${k-}$order algebraic number if and only is the minimal polynomial of ${\alpha}$, ${f(x)=a_nx^n+…+a_1x+a_0, a_n\neq 0}$ have degree ${deg(f)=n, f\in {\mathbb Z}[x]}$.
Definition 5 (Height) Now we define the height of a ${k-}$th order algebraic number as ${H(\alpha):=\max\{\|a_n\|_h,\|a_{n-1}\|_h,…,\|a_0\|_h\}}$, Where
$\displaystyle h(a_i)=\|a_i\|_{\infty} \ \ \ \ \ (11)$
Now we state the conjecture:
Theorem 6 (Swiring-Schimidt conjecture) For all transendental number ${x\in {\mathbb C}}$, there is infinitely ${\alpha}$ are ${k-}$th algebraic number such that:
$\displaystyle |x-\alpha|<\frac{c_k}{H(\alpha)^{k+1}} \ \ \ \ \ (12)$
Where ${c_k}$ is a constant only related to ${k}$ but not ${x}$.
I point out the conjecture is very related to the map:
$\displaystyle F:(x_1,…,x_n) \longrightarrow (\sigma_1(x_1,…,x_n),\sigma_2(x_1,…,x_n),…,\sigma_n(x_1,…,x_n)) \ \ \ \ \ (13)$
Where ${\sigma_k(x_1,…,x_n)=\sum_{1\leq i_1<…<i_k\leq n}\Pi_{j=1}^kx_{i_1}x_{i_2}…x_{i_k}}$ is the ${k-}$th symmetric sum.
Remark 4 ${F}$ is a map ${{\mathbb C}^n\rightarrow {\mathbb C}^n}$, what we consider is its inverse, ${G=F^{-1}}$, but ${G}$ is not smooth, it occur singularity when ${x_i=x_j}$ for some ${i\neq j}$. And the map, as we know, the singularity depend on the quantity ${\Pi_{1\leq i< j\leq n}(x_i-x_j)}$.
Remark 5 I then say something about the geometric behaviour of the map ${G}$, as we know, what we have in mind is consider the map ${G}$ as a distortion ${{\mathbb C}^n\rightarrow {\mathbb C}^n}$, Then ${H(\alpha)}$ is just the pullback of the canonical metric on ${{\mathbb C}}$(morally) to ${{\mathbb C}}$.