Dirichlet hyperbola method

A pdf version is Dirichlet hyperbola method.

1. Introduction

Theorem 1

$\sum_{1\leq n\leq x}d(n)=\sum_{1\leq n\leq x}[\frac{x}{n}]=xlogx+(2\gamma-1) x+O(\sqrt{x}) \ \ \ \ \ (1)$

Remark 1 I thought this problem initial 5 years ago, cost me several days to find a answer, I definitely get something without the argument of Dirchlet hyperbola method and which is weaker but morally the same camparable with the result get by Dirichlet hyperbola method.

Remark 2 How to get the formula:

$\sum_{1\leq n\leq x}d(x)=\sum_{1\leq n\leq x}[\frac{x}{n}]? \ \ \ \ \ (2)$

In fact,

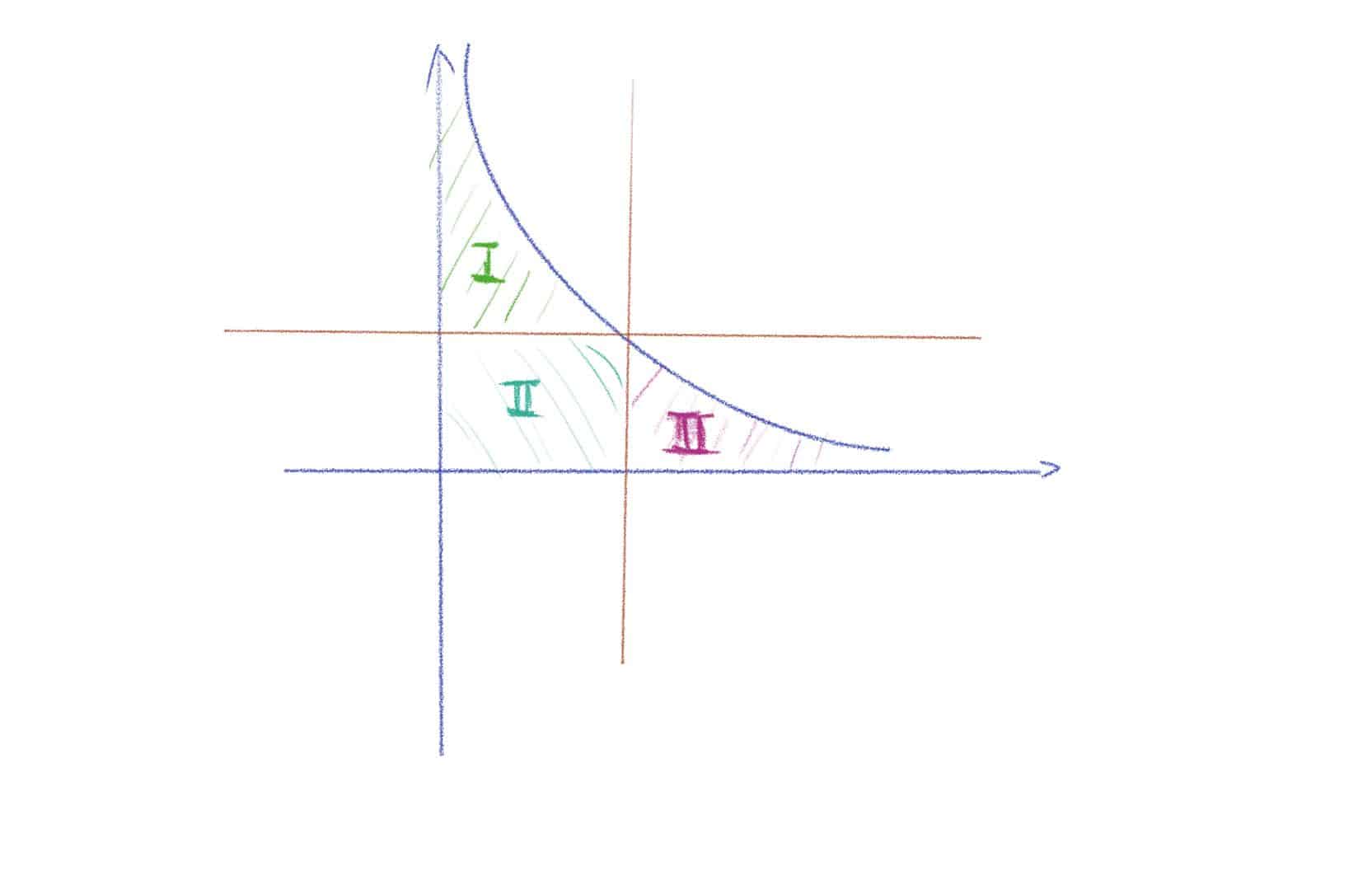
$\sum_{1\leq n\leq x}d(x)=\sum_{1\leq ab\leq x}1=\sum_{1\leq n\leq x}[\frac{x}{n}]\ \ \ \ \ (3)

Which is the integer lattices under or lying on the hyperbola ${\{(a,b)|ab=x\}}.$

Remark 3 By trivial argument, we can bound the quantity as following way,

$\begin{array}{rcl} \sum_{1\leq n\leq x}[\frac{x}{n}] & = & \sum_{1\leq ab\leq x}1\\ & = & x\sum_{i=1}^x\frac{1}{i}-\sum_{i=1}^x\{\frac{x}{i}\}\\ & = &xlnx+\gamma x+O(x) \end{array}$

The error term is ${O(x)}, which is too big. But fortunately we can use the symmetry of hyperbola to improve the error term.

Proof:

$\begin{array}{rcl} \sum_{1\leq n\leq x}d(n) & = & \sum_{ab\leq x}1\\ & = & \sum_{a\geq \sqrt{x}}[\frac{x}{b}]+\sum_{b\geq \sqrt{x}}[\frac{x}{a}]-\sum_{1\leq a,b\leq \sqrt{x}}1\\ & = & xlogx+(2\gamma-1)x+O(\sqrt{x}) \end{array}$

$\Box

Theorem 2

Given a natural number k, use the hyperbola method together
with induction and partial summation to show that

$\sum_{n\leq x}d_k(n) = xP_k(log x) + O(x^{1-\frac{1}{k}+\epsilon}), n\leq x \ \ \ \ \ (4)$

where ${P_k(t)} denotes a polynomial of degree ${k-1} with leading term ${\frac{t^{k-1}}{(k-1)!}}.

Remark 4 $l{P_k(x)}$ is the residue of ${\zeta(s)^kx^ss^{-1}}$ at ${s=1}.

Proof:

We can establish the dimension 3 case directly, which is the following asymptotic formula,

$\sum_{1\leq xy\leq n}[\frac{n}{xy}]=xP_2(logx)+O(x^{1-\frac{1}{3}+\epsilon}) \ \ \ \ \ (5)$

The approach is following, we first observe that

$\sum_{1\leq xy\leq n}[\frac{n}{xy}]=\sum_{xyz\leq n}1 \ \ \ \ \ (6)$

The problem transform to get a asymptotic formula for the lattices under 3 dimension hyperbola. The first key point is, morally ${([n^{\frac{1}{3}}],[n^{\frac{1}{3}}],[n^{\frac{1}{3}}])}$ is the central point under the hyperbola.

Then we can divide the range into 3 parts, and try to get a asymptotic formula for each part then add them together. Assume we have:

1. $ {A_x=\sum_{1\leq r\leq [n^{\frac{1}{3}}]}\sum_{1\leq yz\leq [n^{\frac{2}{3}}]}[\frac{r}{yz}]}.$
2. ${A_y=\sum_{1\leq r\leq [n^{\frac{1}{3}}]}\sum_{1\leq xz\leq [n^{\frac{2}{3}}]}[\frac{r}{yz}]}.$
3. ${A_z=\sum_{1\leq r\leq [n^{\frac{1}{3}}]}\sum_{1\leq xy\leq [n^{\frac{2}{3}}]}[\frac{r}{yz}]}.$

Then the task transform to get a asymptotic formula,

$A_x=A_y=A_z=xQ_2(logx)+O(x^{1-\frac{1}{3}+\epsilon}) \ \ \ \ \ (7)$

But we can do the same thing for ${\sum_{1\leq yz\leq [n^{\frac{2}{3}}]}[\frac{r}{yz}]}$ and then integral it. This end the proof. For general ${k\in {\mathbb N}}$, the story is the same, by induction.

Induction on ${k}$ and use the Fubini theorem to calculate ${\sum_{x_1…x_r\leq n}\frac{n}{x_1…x_r},\forall 1\leq r\leq k}. $\Box

There is a major unsolved problem called Dirichlet divisor problem.

$\sum_{n\leq x}d(n) \ \ \ \ \ (8)

What is the error term? The conjecture is the error term is ${O(x^{\theta}), \forall \theta>\frac{1}{4}}$, it is known that ${\theta=\frac{1}{4}}$ is not right.

Remark 5

To beats this problem, need some tools in algebraic geometry.

2. Several problems

${\forall k\in {\mathbb N}}$, is there a asymptotic formula for ${\sum_{t=1}^n\{\frac{kn}{t}\}}$ ?

${\forall k\in {\mathbb N}}$, ${f(n)}$ is a polynomial with degree ${k}$, is there a asymptotic formula for ${\sum_{t=1}^n\{\frac{f(n)}{t}\}}$ ?

${\forall k\in {\mathbb N}}$, ${g(n)}$ is a polynomial with degree ${k}$, is there a asymptotic formula for ${\sum_{t=1}^n\{\frac{n}{g(t)}\}}$ ?

Theorem 3 ${k\in {\mathbb N}}$, then we have

$\lim_{n\rightarrow \infty}\frac{\{\frac{kn}{1}\}+\{\frac{kn}{2}\}+…+\{\frac{kn}{n}\}}{n}=k(\sum_{i=1}^k\frac{1}{i}-lnk-\gamma) \ \ \ \ \ (9)$

Proof:

$\begin{array}{rcl} \frac{\{\frac{kn}{1}\}+\{\frac{kn}{2}\}+…+\{\frac{kn}{n}\}}{n} & = & \frac{\sum_{i=1}^k\frac{kn}{i}-\sum_{i=1}^n[\frac{kn}{i}]}{n}\\ & = & k(lnn+\gamma +\epsilon_n)-\frac{\sum_{i=1}^{kn}[\frac{kn}{i}]-\sum_{i=n+1}^{kn}[\frac{kn}{i}]}{n} \end{array}

$\Box