Introduction
the statement of Hilbert’s 16th problem:
$ H(n)<\infty?$
definition of $ H(n)=max$
Limit cycle:
Try beginning with Bendixon-Poincaré theorem, which is classical stuff and belongs to a lot of textbooks on vector fields.
Affine invariance
The number of limit cycle is invariant under affine map.
Classification of singular point
Bezout theorem
Example
1.$ \frac{dx}{dt}=y,\frac{dy}{dt}=x$.The graph is just like:

2.$ \frac{dx}{dt}=x^2+y^2,\frac{dy}{dt}=x-y$.The graph is just like:
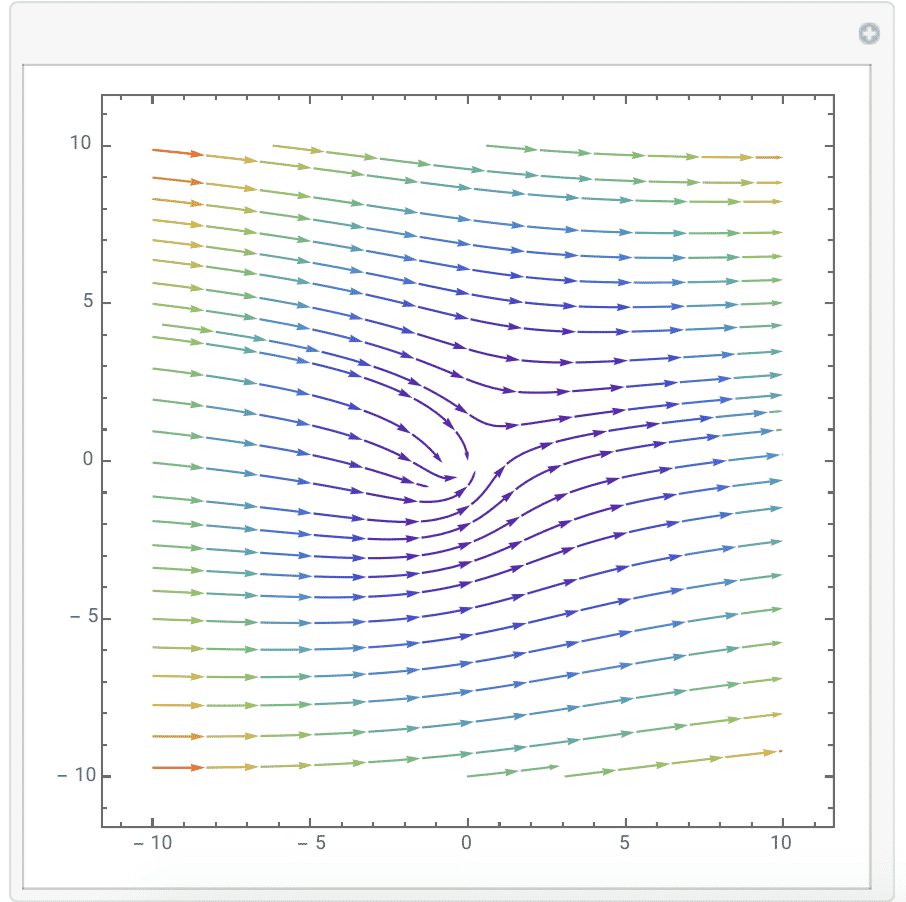
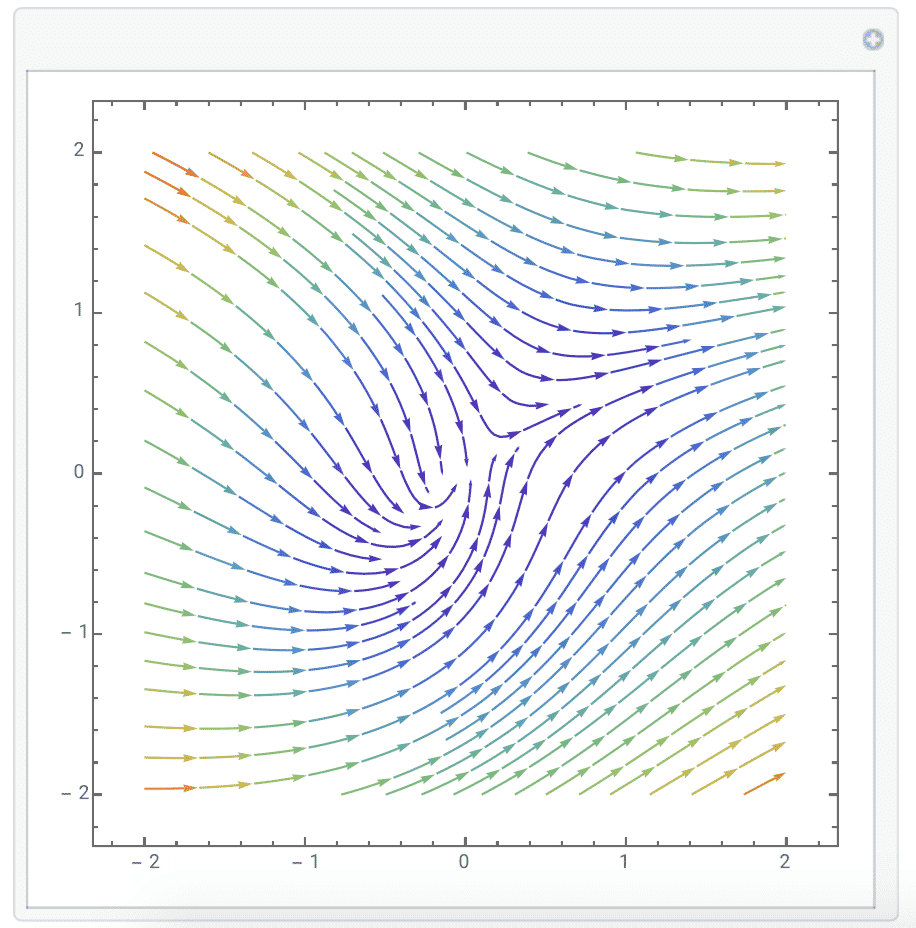
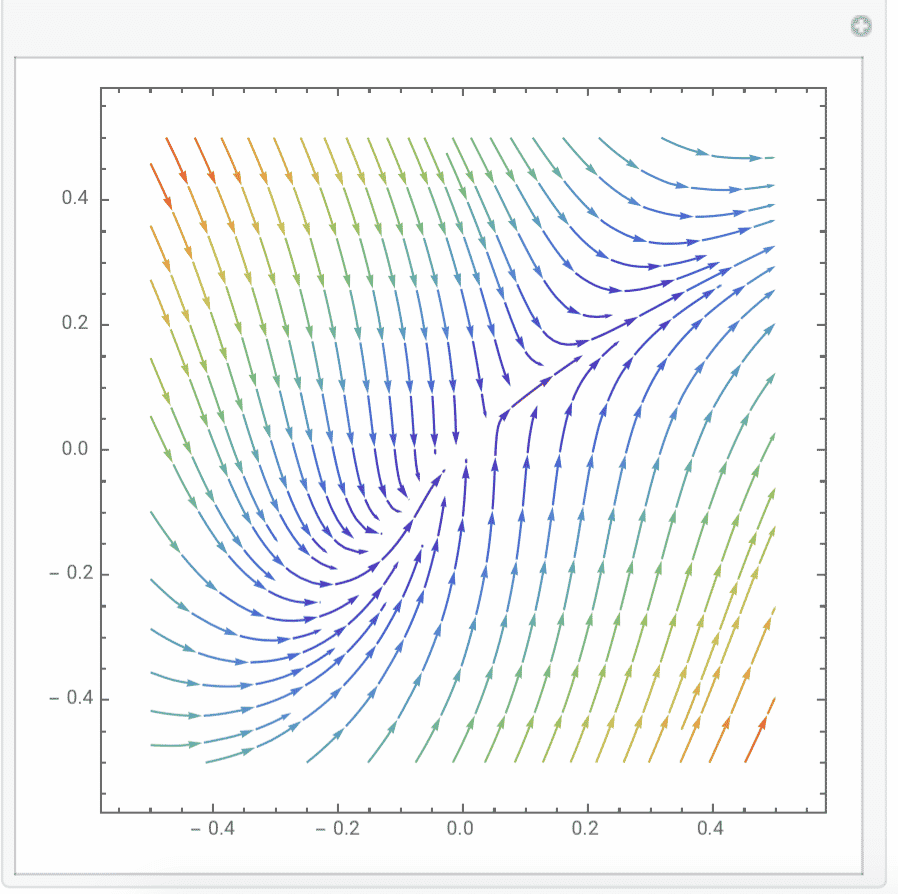
3.$ \frac{dx}{dt}=x^2-y^2,\frac{dy}{dt}=5-y$.The graph is just like:
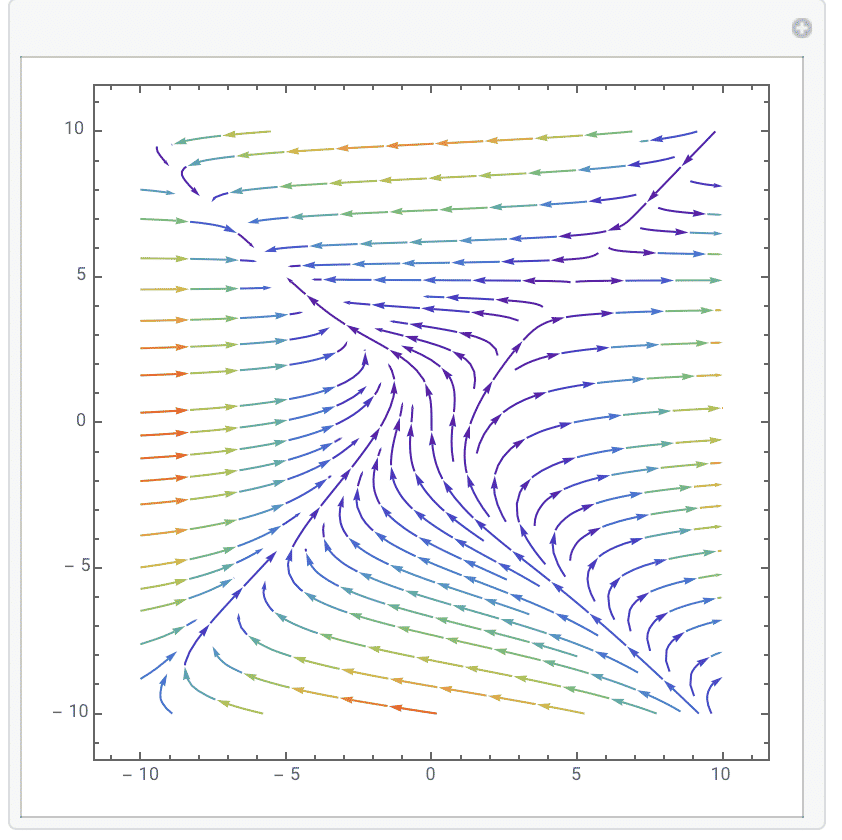
4.$ \frac{dx}{dt}=x^2-y^2,\frac{dy}{dt}=-y$.The graph is just like:
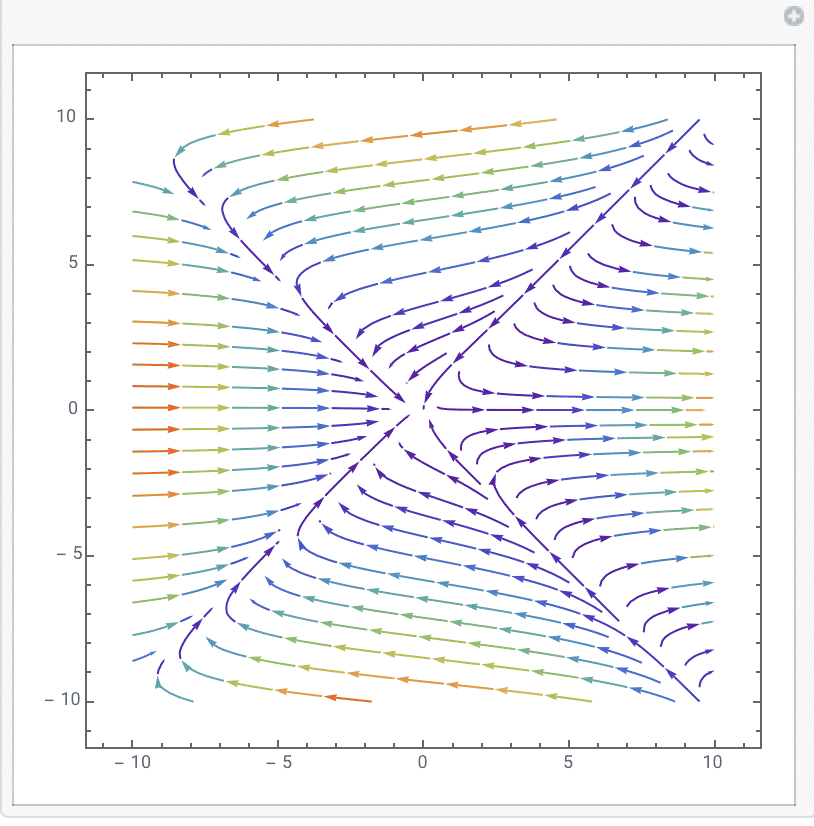
5.$ \frac{dx}{dt}=x^3-y^3,\frac{dy}{dt}=5-y$.The graph is just like:
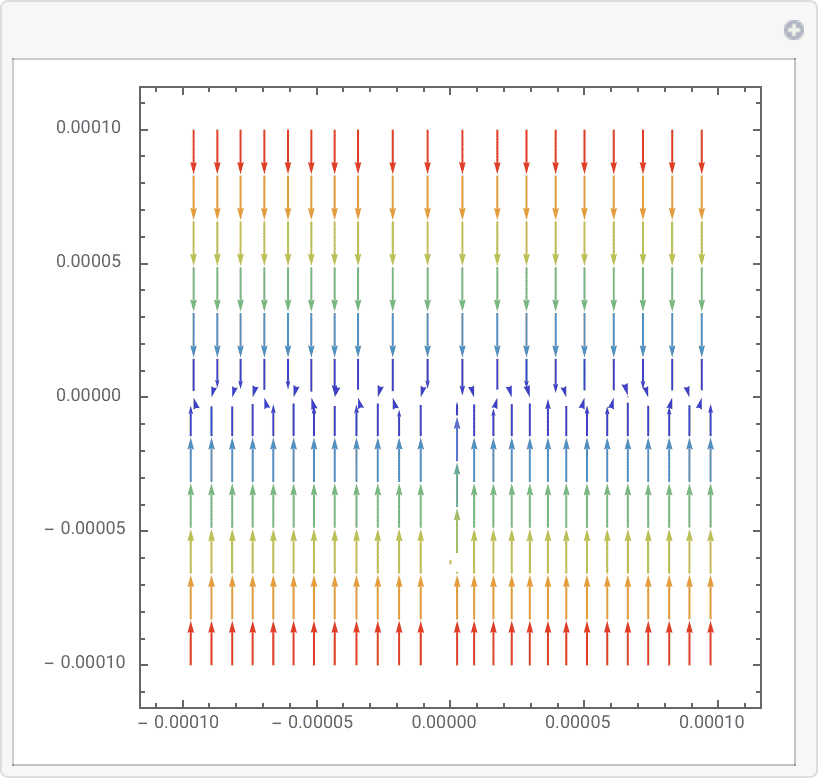
6.$ \frac{dx}{dt}=y^2-x^2+1,\frac{dy}{dt}=y$. The graph of it is just like:
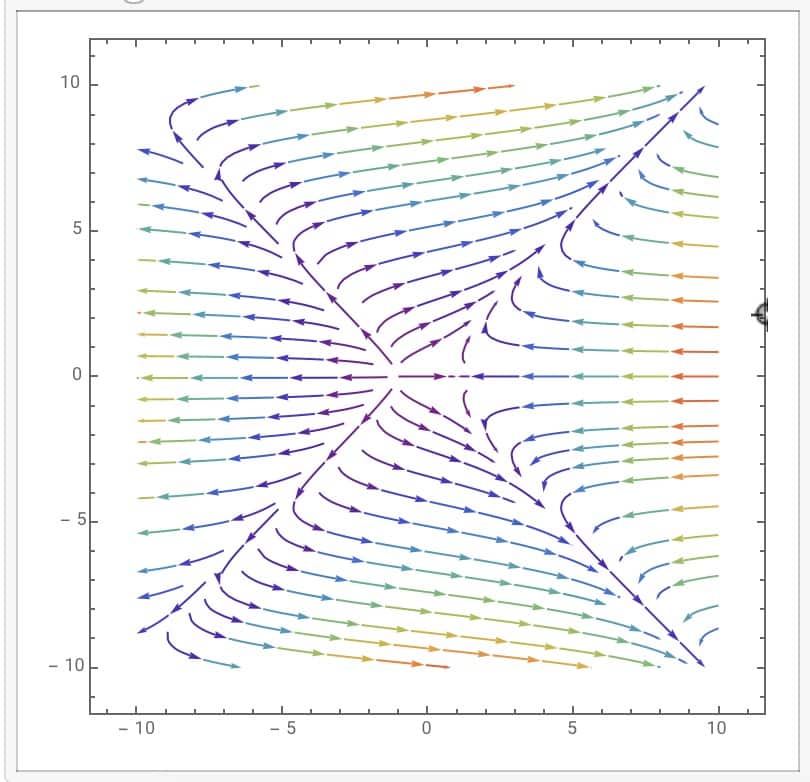
Now we try to explain the phenomenon we see. At first we can see there is no limit cycle in the picture. The bifurcation place is just the place $ \frac{dx}{dt}=0\ or \frac{dy}{dt}=0$ and is just like 3 lines. And there are two singularity $ (-1,0),(1,0)$.
7.$ \frac{dx}{dt}=y,\frac{dy}{dt}=y-x^2-x^2y$
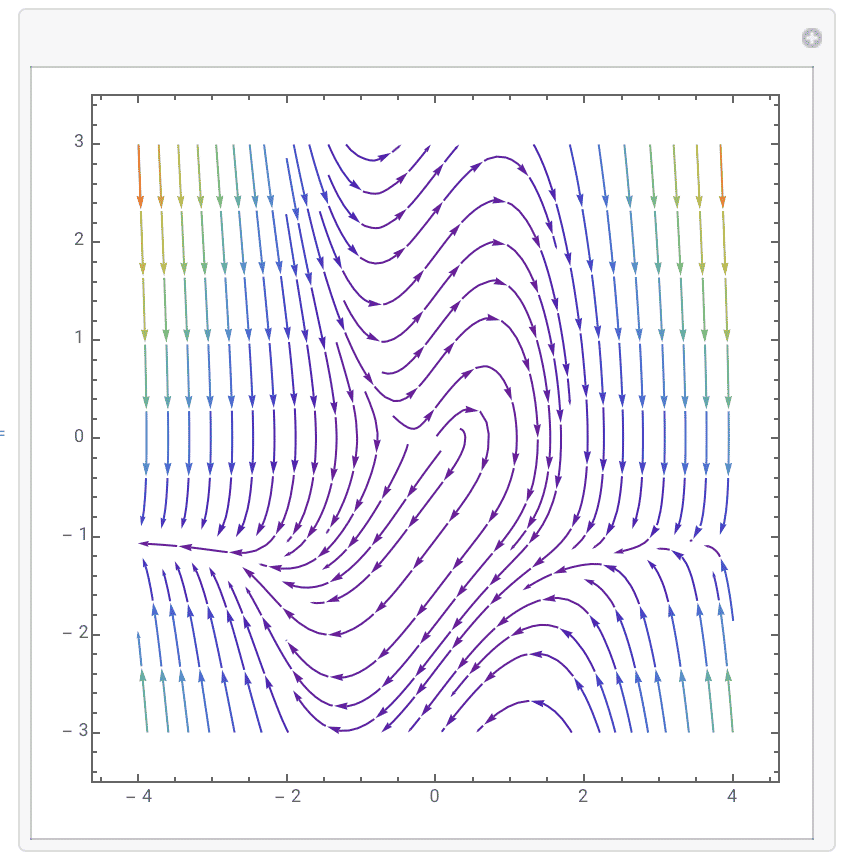
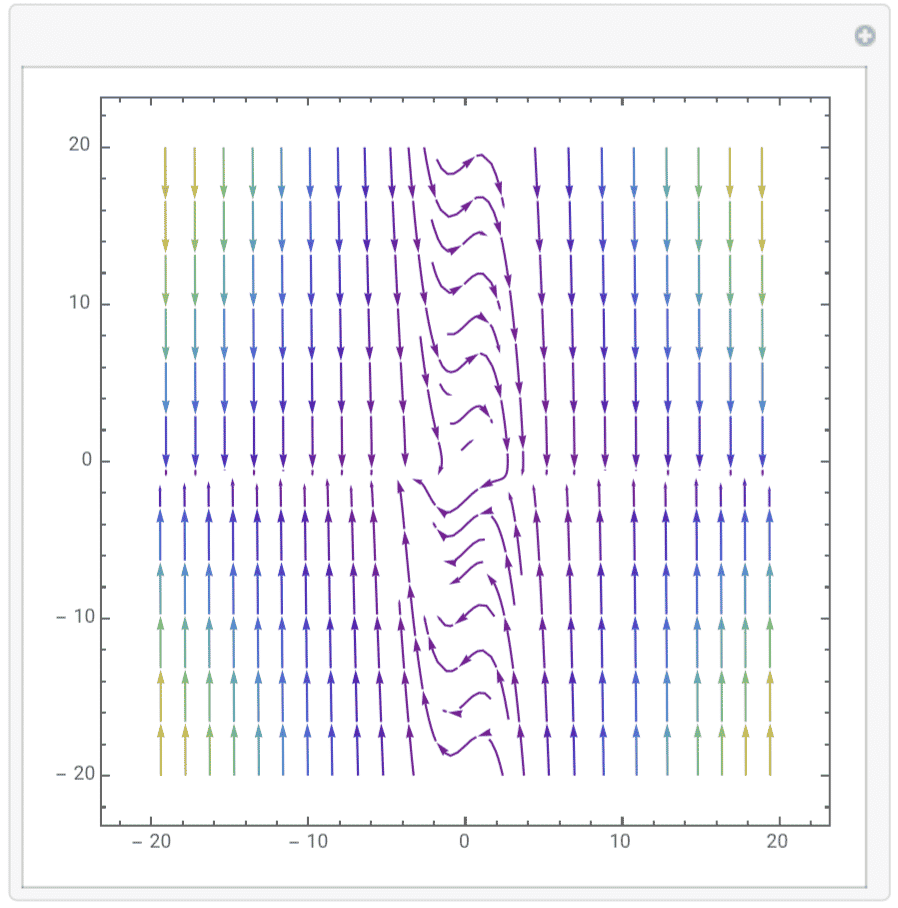
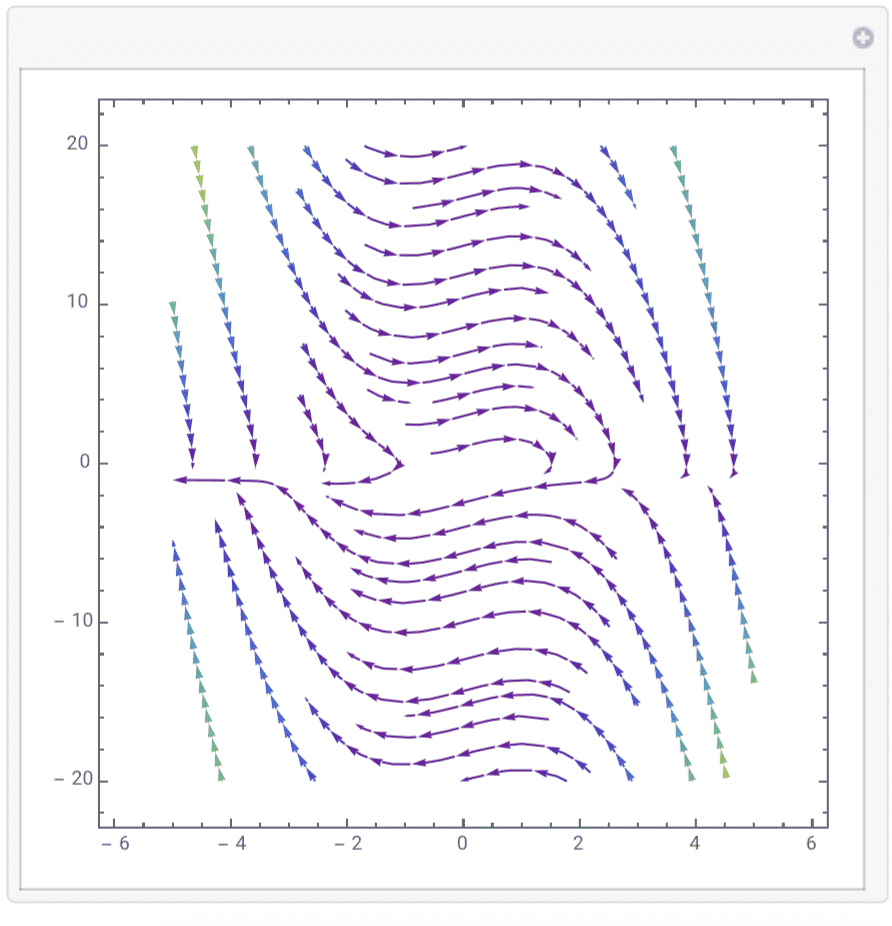
8.$ \frac{dx}{dt}=y,\frac{dy}{dt}=y-x-x^2y$:
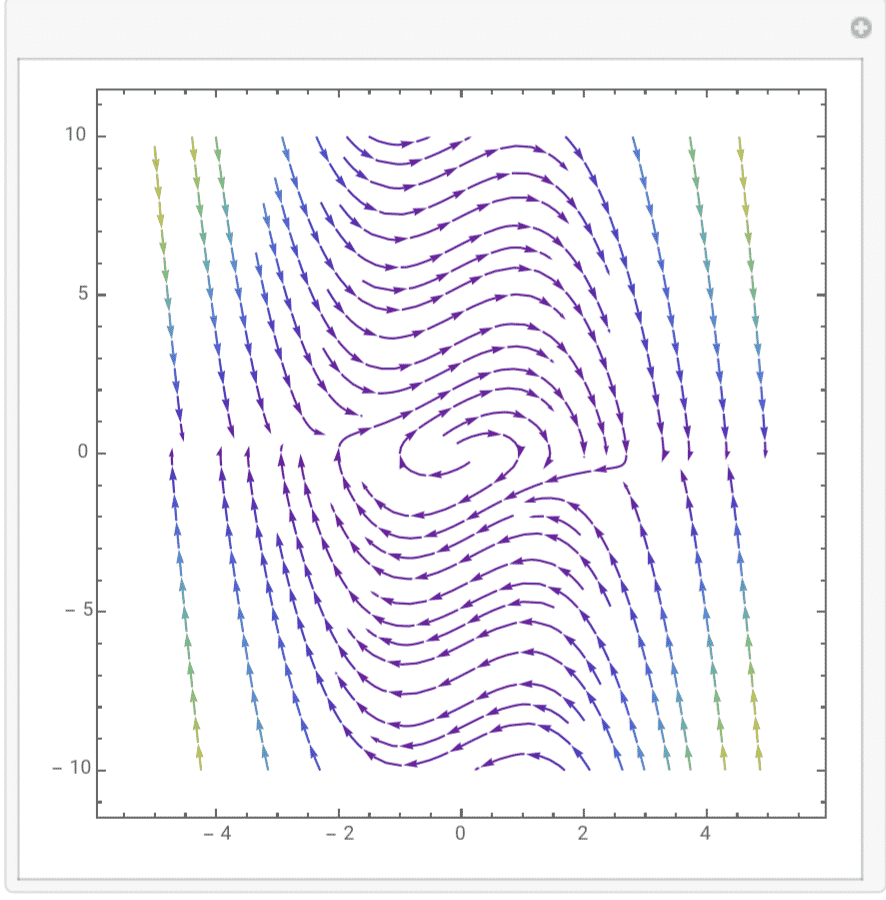
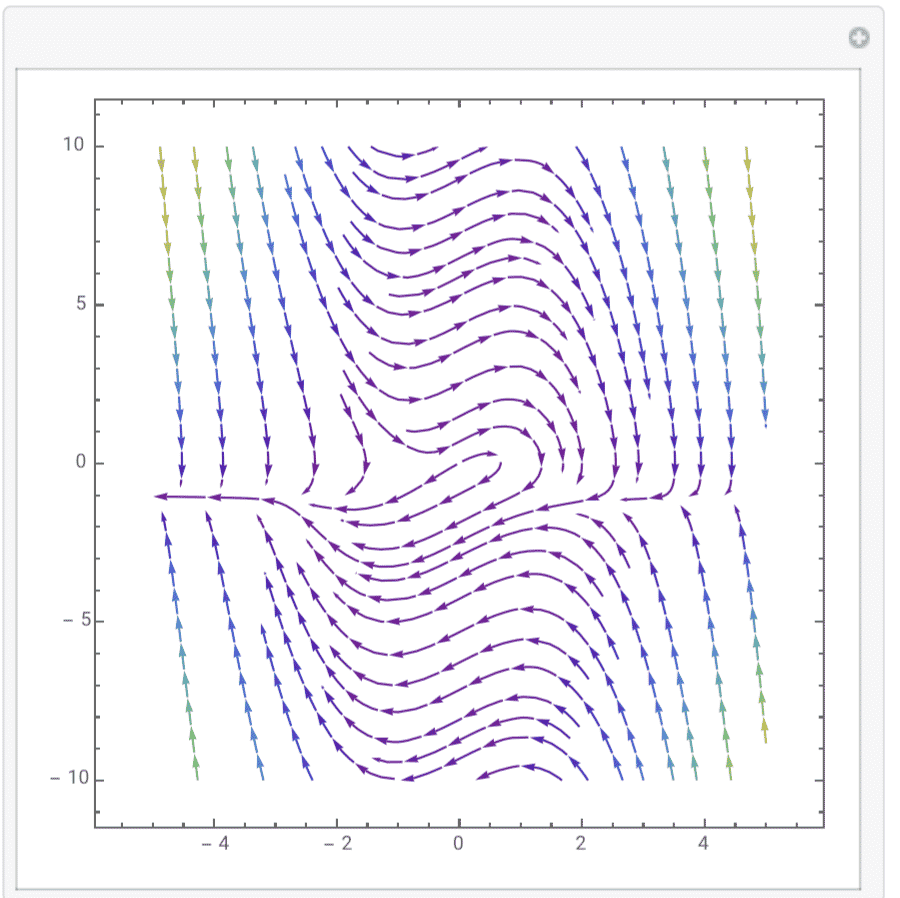
9.$ \frac{dx}{dt}=y(y-3),\frac{dy}{dt}=(y-3-x-x^2y)(y-x-x^2y)$:

exist 2 limits cycles.
10.$ \frac{dx}{dt}=y(y-3)(y-5),\frac{dy}{dt}(y-5-x-x^2y)(y-3-x-x^2y)(y-x-x^2y)$
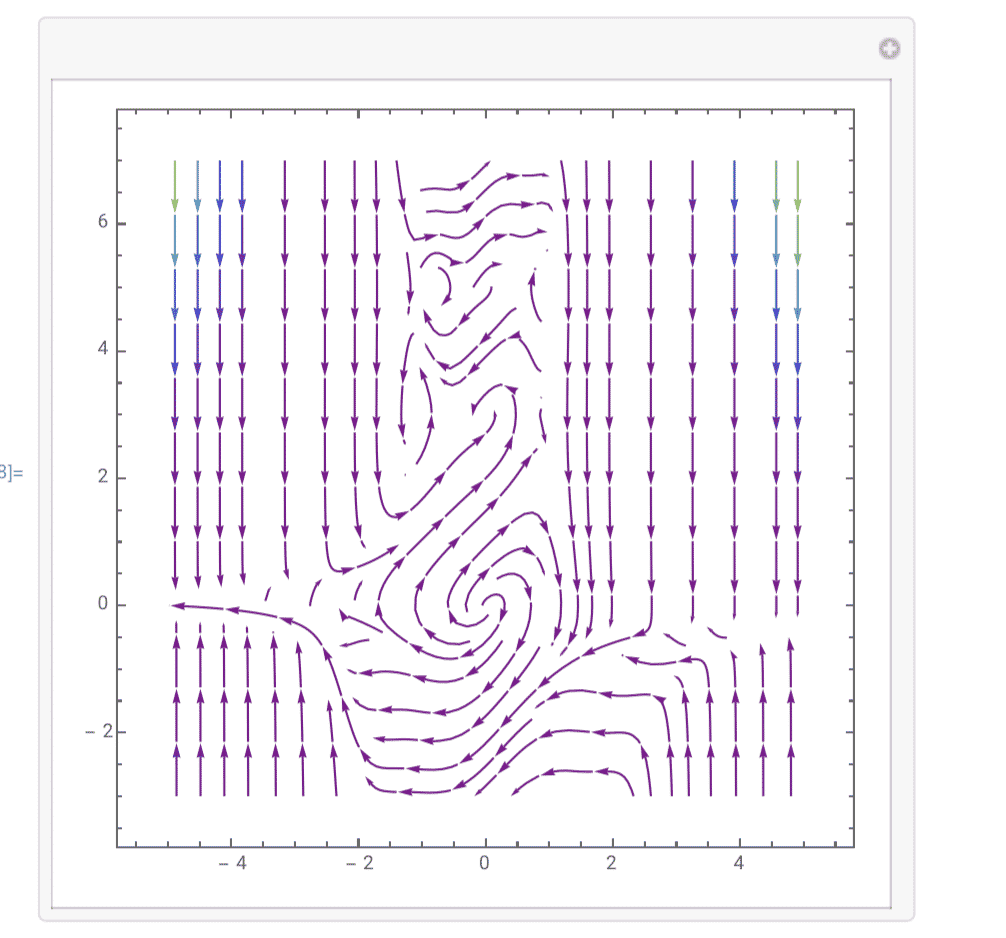
Tree structure
In general, the lower bound of $ H(n)$ is established. first $ H(n)=O(n^2)$ by Otrokov,and later proved to be $ H(x)=O(ln(n)n^2)$.
If right, this upper bound estimate is combine of two things:
1.every limit cycle do not intersect.
2.every unclear limit cycle contain a singularity.
Rough strategy attack Hilbert 16th problem
Step1:
The first step is to do some simplify, we know the number of limit cycles do not change under a affine map $ (x,y)\to (\hat x,\hat y)=(x,y)A$, where A is a nonsingular 2*2 matrix. So we could classify the topological graph of the dynamic system.
Step2:
Classification the singularity under affine map, and investigate the topological graph of the topological graph of the singularity by floer cohomology. There is only finite type and we could focus on them one by one.
Every color in the graph is an area $P,Q$ do not have same component in it. And the boundary of areas is just the same component of $ P,Q$ if it exists.
Step3:
Bezout theorem tell us if two polynomials $ P(x,y), Q(x,y)$ do not have same connected component then the intersection $ I_{P,Q}\leq deg(P)deg(Q)$. And we can divide the space $ R^2$ into finite parts, $ P(x,y),Q(x,y)$ restrict to every part do not have the same component. And we have a upper bound control on the number of part when $ \max\{deg(P(x,y)),deg(Q(x,y))\} \leq n$. A easy arrive bound could be $ 4^n$.
Step4:
Now we focus ourself on 1 part where $ P(x,y),Q(x,y)$ do not have same component on it. Now we begin to proof there will be a relationship between the limit cycle, very like a tree structure, it will combine with the following two thing:
- Every limit cycle contains at least one singularity or one smaller limit cycle inside it.
2. Every pair of limit cycle $ (A,B)$, $ A,B$ are limit cycle and $ A$ is inside of $ B$, then there is at least one singularity or another limit cycle contain in $ \Omega$.
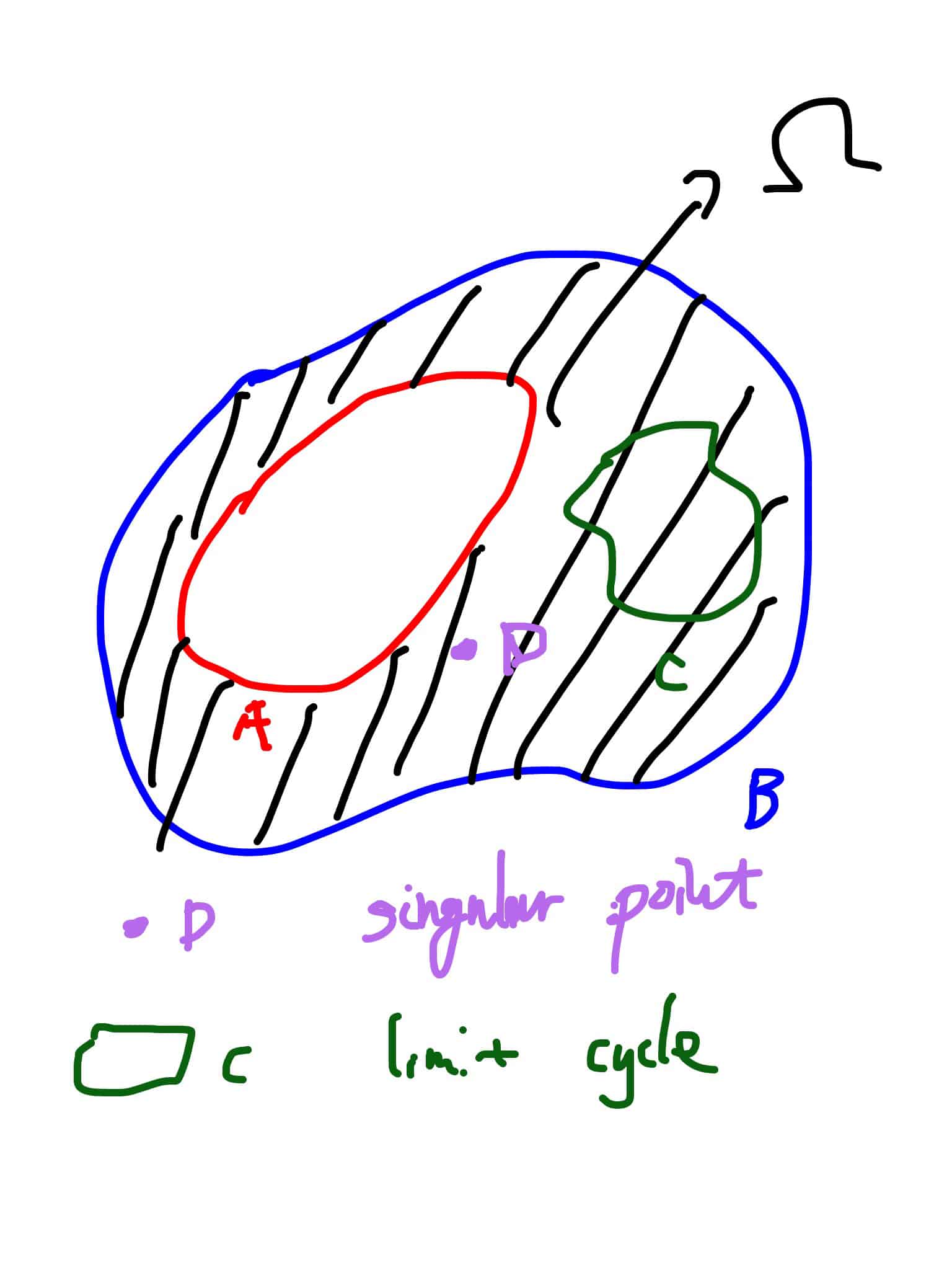
This kind of topological result will lead to a upper bound of number of limit cycle and end the proof of Hilbert 16th problem.
Planar polynomial vector field for a harmonic pair of polynomials
In this case you can consider the heat equation $ \partial_t u(z,t)=\Delta u(z,t)$. If the number of the limit cycle change, it must be the time to pass a singularity. and take $ t=\infty$, the dynamic system coverage to a very simlpe one and in particular it do not have limit cycle. So we need only look at the moments passing singularity.
Has the system of ODEs:
$ \frac{dx}{dt}=P(x,y)\\
\frac{dy}{dt}=Q(x,y)$
been studied for the special case of the polynomials $ P$ and $ Q$ being a harmonic pair, i.e. the real and imaginary part of a holomorphic polynomial $ F=F(z)$, $ z=x+iy$?
I am looking to learn a bit about (complex) ODEs and their interplay with algebraic geometry by some examples, but I couldn’t find anything on this special case in Ilyashenko’s survey on Hilbert 16 (I guess this case is too special and/or not very interesting as far as Hilbert 16 is concerned).
Nontheless, it seems very natural. If we set $ \gamma(t)=x(t)+iy(t)$, this amounts to the equation $ \int_{\gamma_t}\frac{dz}{F(z)}=t$
where $ \gamma_t$ is the curve $ \gamma$ “truncated” at $ t$ and the RHS is in particular **real**. This can be taken further, for example by assuming $ \gamma$ is closed and using the residue theorem to obtain constraints on (the coefficients of) $ F$.
First, this case is totally uninteresting regarding Hilbert XVI. Indeed, there are no limit cycles in such systems. The $ \alpha / \omega$-limit of a trajectory is either a point or a non-isolated cycle (center case).
A singularity at $ a\in \mathbb C$ (*i.e.* a root of $F$) can only be of three types, according to the value of $ F'(a)$:
1. Source/focus: $ F'(a)\notin i\mathbb R$.
2. Center: $ F'(a)\in i\mathbb R_{\neq 0}$.
3. Flower with $ 2k$ petals: $ F'(a)=0$ with multiplicity $ k$.
In addition there is a pole at infinity (if $ \deg(F)>0$) with exactly $ 2\deg(F)$ separatrices, reaching the singularity in finite time. The bassins of attraction / center regions attached to the above singularities are delimited by the separatrices.
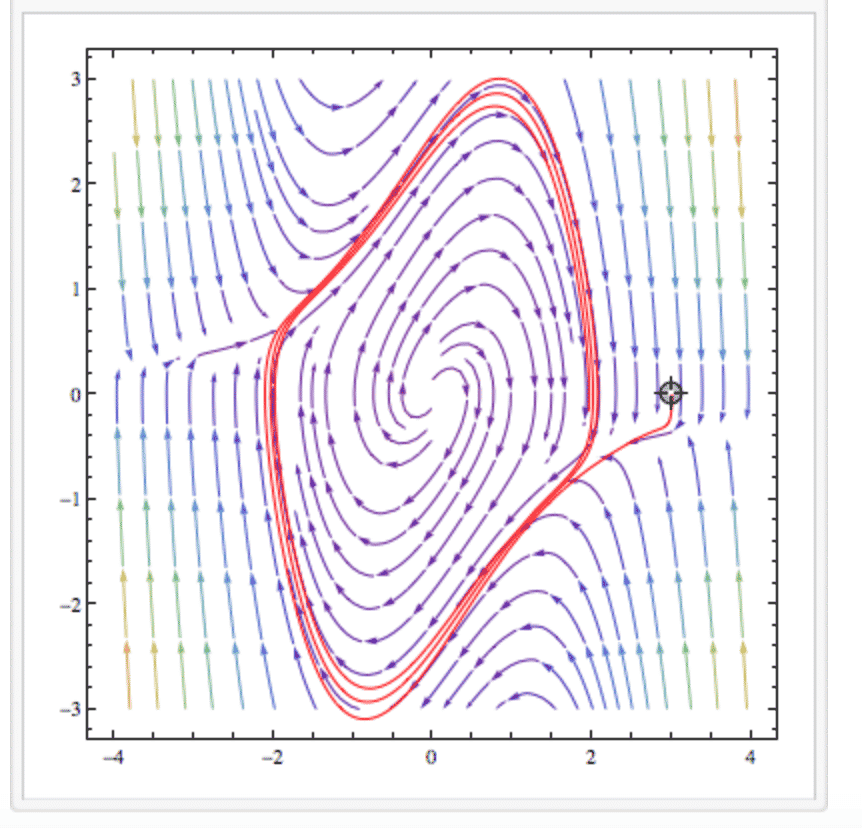
[![enter image description here][2]][2]
S. Smale began to get interested in the question in the early 80’s while laying the foundations for BSS computational model (*The fundamental theorem of algebra and complexity theory*, 1981). He proposed a numerical root solver for polynomials by following the flow of $ \frac{F}{F’}$. This started some works on the topic, for instance by Schub, Tischler, William (*The Newtonian graph of a complex polynomial*, 1988) or Benzinger (*Plane autonomous systems with rational vector fields*, 1991)…
In the case of these vector fields, the topological class is entirely encoded by their Newtonian graph (or the «dual» spinal graph) given by the incidence graph of the $ \alpha / \omega$-limits of trajectories (in red on the picture). The main result for polynomials is that it is a tree. See *e.g.* Sverdlove (*Inverse problems for dynamical systems*,1981) and Schecter, Singer (*A class of vectorfields on $\mathbb S^2$ that are topologically equivalent to polynomial vectorfields*,1985) and Jongen, Jonker, Twilt (*On the classification of plane graphs representing structurally stable rational Newton flows*,1991).
The conformal classification has been initiated by Douady, Estrada and Sentenac (unpublished monograph, 2005) for the generic case (only focus/source singularities) and completed by Branner and Dias (*Classification of complex polynomial vector fields in one complex variable*, 2010). In addition to the combinatorial (topological) invariant, a complex «time-shift» (related to the integrals $ \int_\gamma\frac{1}{F(z)} dz$) is associated to the separatrices, providing a complete conformal invariant.
In that latter context, the function $ \int\frac{1}{F(z)} dz$ is called a Fatou coordinates. It is a rectifying chart for the vector field, and has many interesting dynamical properties.
Notice also the deep and beautiful relationship between spinal graph and *Dessins d’enfants*, as established by Pilgrim (*Polynomial vector fields, dessins d’enfants, and circle packings*,2006), related to [this question](https://mathoverflow.net/questions/118527).

Reference
Classification of Singularities and Bifurcations of Critical Points of Even Functions
E.A.Kudryavtseva, E.Lakshtanov
Classification of the singularity in even degree case.
Adjoint harmonic case have been studied. Look into the recent paper
Langley, J. K. Trajectories escaping to infinity in finite time. Proc. Amer. Math. Soc. 145 (2017), no. 5, 2107–2117, and the reference list in this paper.
They were also studied by physicists:
Bender, Carl M.; Hook, Daniel W.
Complex classical motion in potentials with poles and turning points.
Stud. Appl. Math. 133 (2014), no. 3, 318–336.
EDIT. I forgot to mention this:
B. Branner, K. Dias, Classification of complex polynomial vector fields in
one complex variable, Journal
Journal of Difference Equations and Applications
Volume 16, 2010 – Issue 5-6: