Sarnak conjecture is a conjecture lies in the overlap of dynamic system and number theory. It is mainly focus on understanding the behavior of an entropy zero dynamic system by looking at the correlation of an observable and the Mobius function .
We state it in a rigorous way:
let $ (X,T)$ be an entropy zero topological dynamic system. Let the Mobius function be defined as $ \mu(n)=(-1)^t$, where $ $ is the number of different primes that occur in the decomposition of $ n$.
Then for any continuous function $ f:X\to R$ and $ x\in X$, observable $ \xi(n)=f(T^n(x))$ is orthogonal to the Mobius function; i.e. ,
$ \lim_{N\to \infty}\frac{1}{N}\sum_{n=0}^{N-1}\mu(n)\xi(n)=o(N).$
I mainly focus on the special cases when dynamic system $ X$ is the skew product on $ T^2$ and when the dynamic system which is an interval exchange in $ [0,1]$.
Skew product
For the first one, $ \Theta=(T,T^2)$,$ T:T^2\longrightarrow T^2 $:
$ T(x)=x+\alpha,T(y)=cx+y+h(x)$
$ y_1(n)=T^{n}(x)=x+n\alpha,y_2(n)=T^n(y)=nx+\frac{n(n-1)}{2}\alpha+y+\sum_{n=1}^{N-1}h(x+i\alpha) $, where $ c=1,-1$.
by Bourgain-Ziegelar-Sarnak theorem we know the difficulties is focused on deal with the exponent
$ S_{p,q}(N)=\sum_{n=1}^N\mu(n)e^{\phi(n)+\sum_{m\in Z}e(mx)\hat H(m)(\frac{e(npm\alpha)-1}{e(m\alpha)-1}- \frac{e(nqm\alpha)-1}{e(m\alpha)-1})}$
for all $ p,q$ is suffice large primes pair.
and a much simper case is the affine map:$ T:(x,y)\to (x+\alpha,cx+y+\beta)$ on $ \mathbb T^2$ and the general case $ T:(x_1,…,x_n)\to A(x_1,…,x_n)$ where A is a upper-triangle matrix with diagonal 1; i.e. $ A=I+B$, B is nilpotent. So the sarnak conjecture in this case is reduced to the Davenport estimate on exponent by B-Z-S theorem:
$ |\sum_{n=0}^{N}e^{2\pi if(n)}|\leq c_A\frac{N}{(log N)^A}$, $ \forall A>0$.
Interval exchange map
For the interval exchange map, we can explain it by a composition of rotation of some part of $ S_1$ step by step and with a renormalization process to glue the neighbor rotations.
Now let us explain a little with this interesting dynamic system. We focus in the simplest nontrivial case, which is the 3-interval exchange map. In this case, just consider the permutation of intervals $ I_1,I_2,I_3$, and it is easy to see there is only one case is nontrivial that is permutation: $ I_1\to I_3,I_2\to I_2,I_3\to I_1$. We explain a little more with other trivial cases:
When $ I_1\to I_2,I_2\to I_3,I_3\to I_1$, the interval exchange map is just a rotation for which the Sarnak conjecture is just come from:
$ |\sum_{n=0}^{N}e^{2\pi in\alpha}\mu(n)|=o(N)$, $ \forall \alpha\in R$.
Which is trivial because $ \sum_{n=0}^{N}e^{2\pi in\alpha}\mu(n)=\frac{1-e^{2\pi iN\alpha}}{1-e^{2\pi i\alpha}}$.
For the case $I_1\to I_2, I_2\to I_1, I_3\to i_3$ the map $ T$ is a rotation on $ I_1\cap I_2$ but it is an identity map on $ I_3$ and the orbits of point only lying one of $I_1\cap I_2, I_3$, lying in which one depends on the original point $ x$ we take is lying in which one.
Now we focus on the most difficult situation. It is annoying but it is the obstacle we must get over to go far. Fortunately, it could be explained as in the following picture.
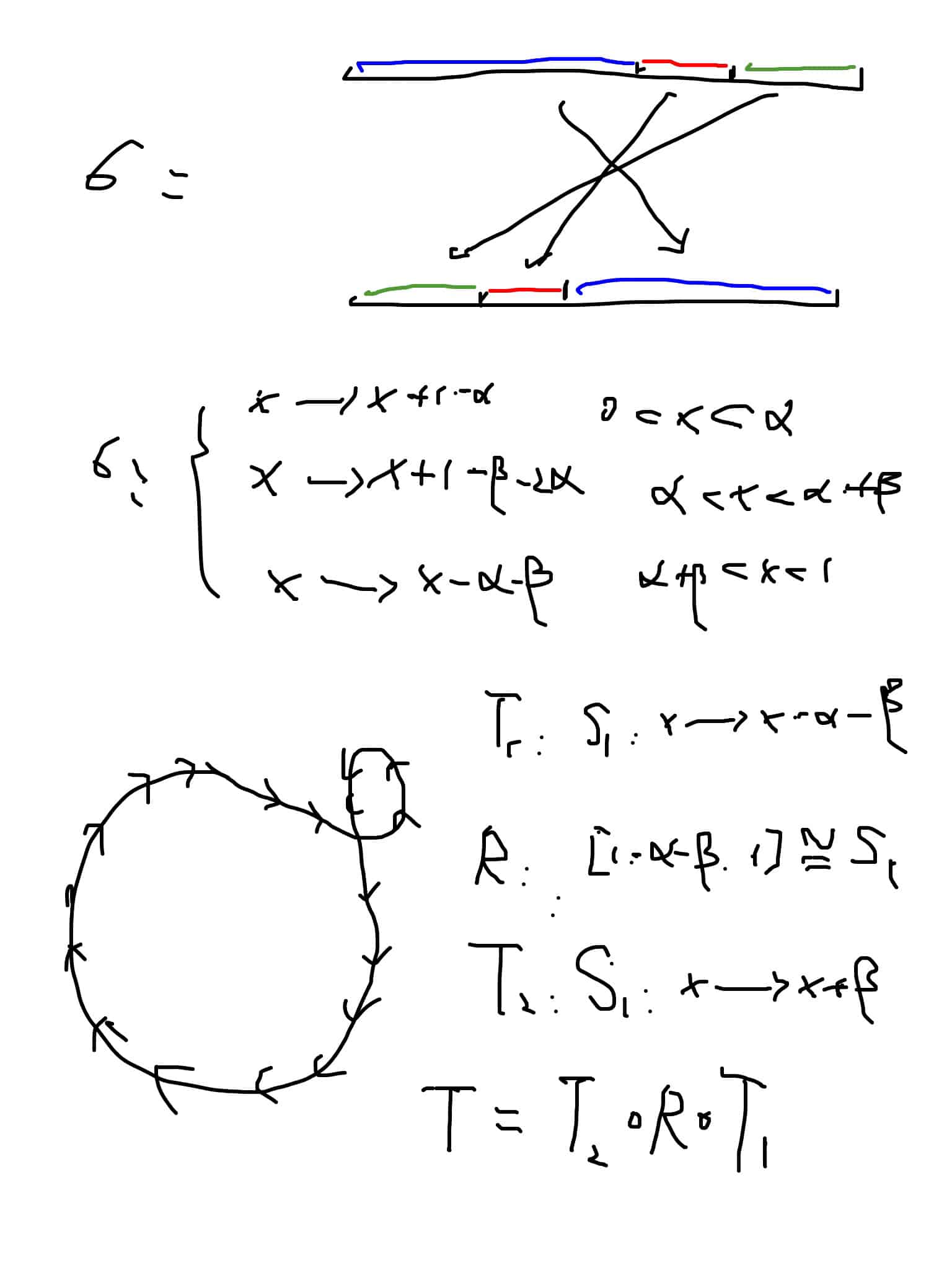
Now we explain what happens in the picture, it is mainly say one identity, which explains how to look 3-interval exchange map as a composition of a rotation map with a renormalization map to glue them. Rotation is a kind of map we have good understanding but we do not understand very well with the renormalization map which glues the two endpoints of $ I_2,I_3$ which are not the common endpoint of them. Then you get two circle glued like a “8” , and $ T_2$ is just rotate one of it and make the other one to be invariant.
Now we roughly could think about what is the thing we need to charge with, it is just:
$ \sum_{n=0}^{N}f((T_1\circ R\circ T_1)^n(x))\mu(n)=o(N)$.
Now we do some calculations with this geometric explanation of interval exchange map.
Let $ A=I_1, B=I_2\cap I_3$, then $ A\cap B=\emptyset, A\cup B=[0,1]$. And $ |A|=\alpha$, $ 0<\beta<|B|$. the rotation $ T_1:x\to x-\alpha$, $ T_2:x\to x+\beta$.
Standard model
Is there a standard model of entropy zero dynamic system?
This problem seems to be too ambitious. But it occurs naturally when I an trying to have a global understanding of the Sarnak conjecture.