Introduction
the statement go isometry inequality is very simple:
$latex \Omega\subset R^n$, iff $latex \Omega$ is a ball, $latex \frac{Vol(\Omega)}{Surf(\Omega)}$ arrive a minimum .
This is a classical problem in variation theory. The difficult is divide into two parts. The first is to create a “flow” which descrement the energy and the “flow” is compatible with the feature of a ball, i.e. every set under the flow will tend to like a “ball”. The second one is to proof there exist a unit in the space $latex surf(\Omega)=constant>0$ make the Energy $latex E(\Omega)=Vol(\Omega)$ arrive a minimum.
Combine this two property we can consult that ball is the set and definitely the only set make the $latex \frac{Vol(\Omega)}{Surf(\Omega)}$ arrive the minimum.
first difficulties
The energy $E(\Omega)$ is scaling invariance. The first difficult could divide into two part:
Restrict to convex set
the first is to deform a set into a convex set and proof this process would not lower $latex \frac{Vol(\Omega)}{Surf(\Omega)}$ . This could been a little subtle. and the way I image could make sense is just like the following transform:
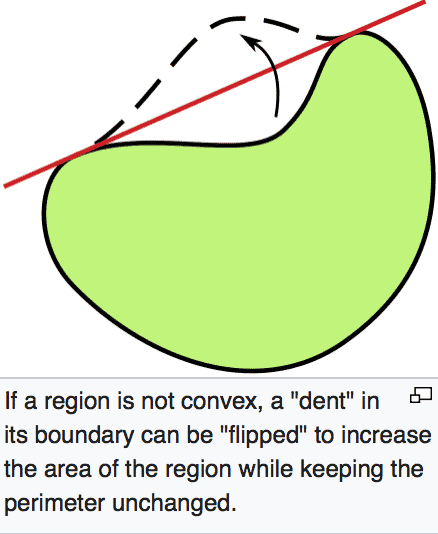
but this process is harder in higher dimension, for example:
Convex set to a ball
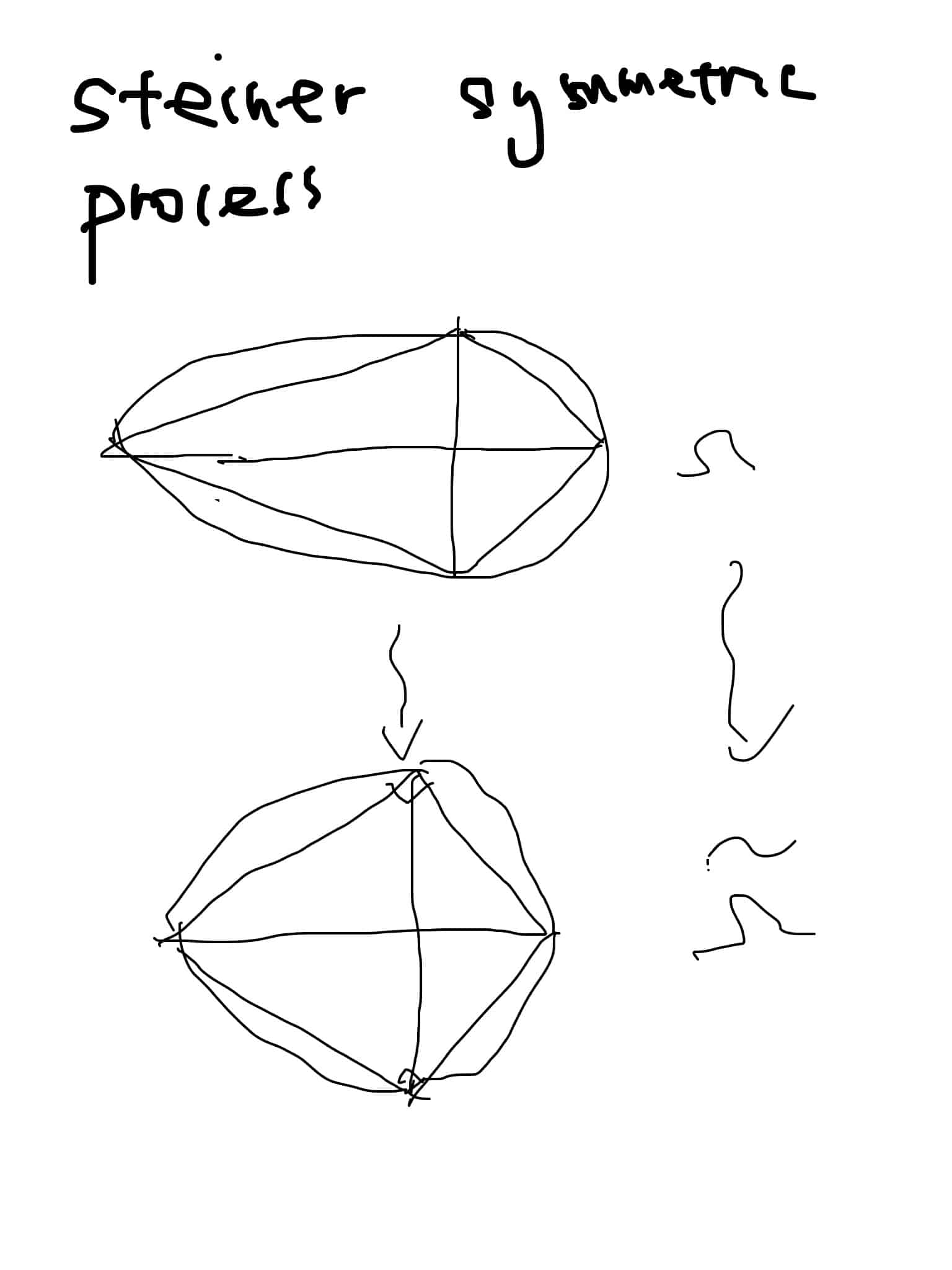
Steiner symmetric process.
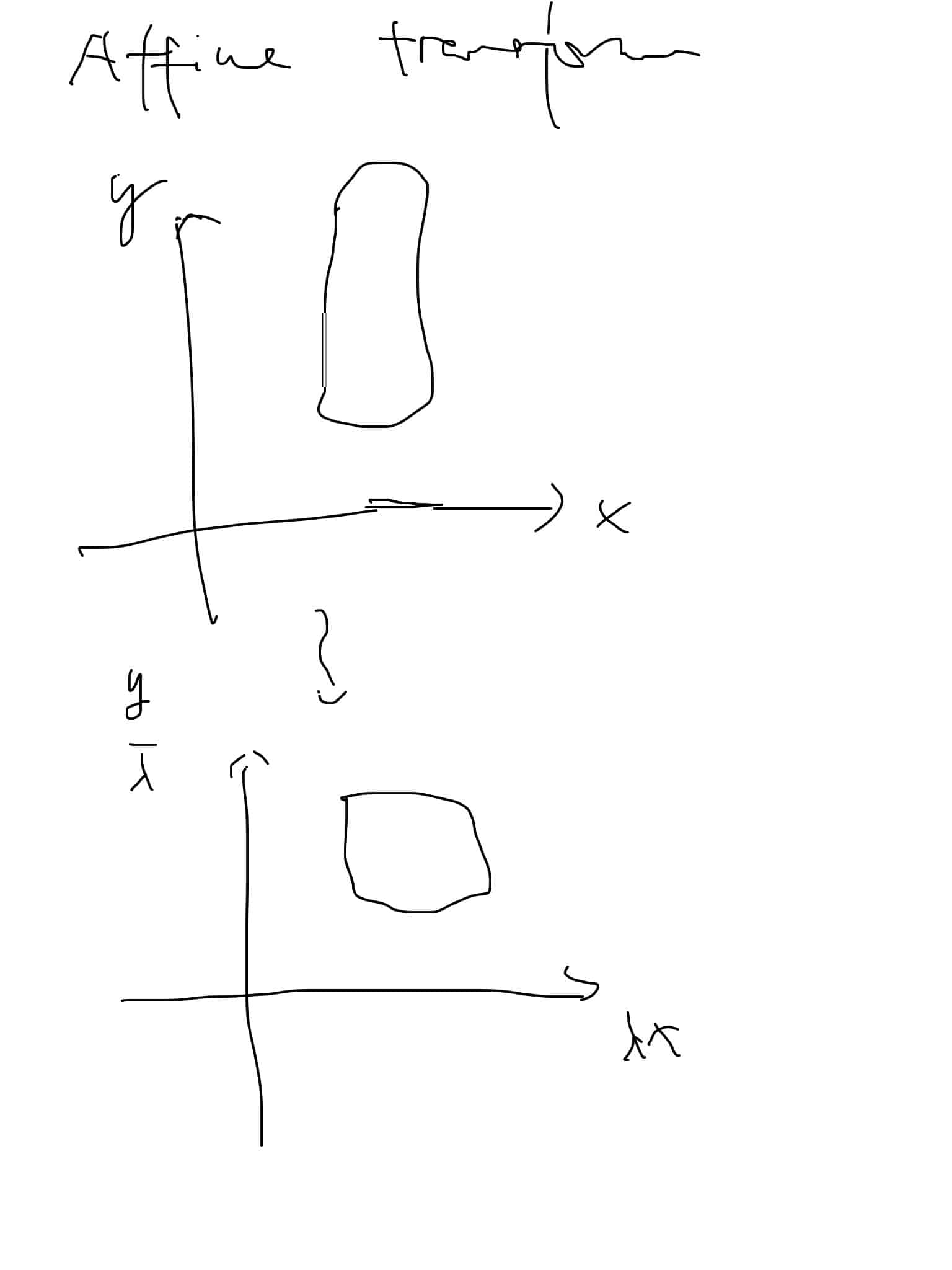
Affine transform
Minkowski–Steiner formula
In mathematics, the Minkowski–Steiner formula is a formula relating the surface area and volume of compact subsets of Euclidean space. More precisely, it defines the surface area as the “derivative” of enclosed volume in an appropriate sense.
The Minkowski–Steiner formula is used, together with the Brunn–Minkowski theorem, to prove the isoperimetric inequality. It is named after Hermann Minkowski and Jakob Steiner.
Statement of the Minkowski-Steiner formula
Let $latex n \geq 2$, and let $latex A \subsetneq \mathbb{R}^{n}$ be a compact set. Let $latex \mu (A)$ denote the [[Lebesgue measure]] (volume) of $latex A$. Define the quantity $latex \lambda (\partial A)$ by the ”’Minkowski–Steiner formula”’:
$latex \lambda (\partial A) := \liminf_{\delta \to 0} \frac{\mu \left( A + \overline{B_{\delta}} \right) – \mu (A)}{\delta}$
where:
$latex \overline{B_{\delta}} := \left\{ x = (x_{1}, \dots, x_{n}) \in \mathbb{R}^{n} \left| | x | := \sqrt{x_{1}^{2} + \dots + x_{n}^{2}} \leq \delta \right. \right\}$
denotes the [[closed ball]] of [[radius]] $latex \delta > 0$, and:
$latex A + \overline{B_{\delta}} := \left\{ a + b \in \mathbb{R}^{n} \left| a \in A, b \in \overline{B_{\delta}} \right. \right\}$
is the [[Minkowski sum]] of $latexA$ and $latex \overline{B_{\delta}}$, so that:
$latex A + \overline{B_{\delta}} = \left\{ x \in \mathbb{R}^{n} | |x – a| \leq \delta \mbox{ for some } a \in A \right\}$.
Surface measure
For “sufficiently regular” sets $latex A$, the quantity $latex \lambda (\partial A)$ does indeed correspond with the $latex (n – 1)$-dimensional measure of the [[boundary (topology)|boundary]] $latex \partial A$ of $latex A$. See Federer (1969) for a full treatment of this problem.
Convex sets
When the set $latex A$ is a [[convex set]], the [[limit inferior|lim-inf]] above is a true [[Limit of a sequence|limit]], and one can show that
:$latex \mu \left( A + \overline{B_{\delta}} \right) = \mu (A) + \lambda (\partial A) \delta + \sum_{i = 2}^{n – 1} \lambda_{i} (A) \delta^{i} + \omega_{n} \delta^{n}$,
where the $latex \lambda_{i}$ are some [[continuous function]]s of $latex A<$ (see [[quermassintegral]]s) and $\omega_{n}$ denotes the measure (volume) of the [[unit ball]] in $latex \mathbb{R}^{n}$:
:$latex \omega_{n} = \frac{2 \pi^{n / 2}}{n \Gamma (n / 2)}$,
where $latex \Gamma$ denotes the [[Gamma function]].
==Example: volume and surface area of a ball==
Taking $latex A = \overline{B_{R}}$ gives the following well-known formula for the surface area of the [[sphere]] of radius $latex R$, $latex S_{R} := \partial B_{R}$:
:$latex \lambda (S_{R}) = \lim_{\delta \to 0} \frac{\mu \left( \overline{B_{R}} + \overline{B_{\delta}} \right) – \mu \left( \overline{B_{R}} \right)}{\delta}$
::$latex = \lim_{\delta \to 0} \frac{[ (R + \delta)^{n} – R^{n} ] \omega_{n}}{\delta}$
::$latex = n R^{n – 1} \omega_{n}$,
where $latex \omega_{n}$ is as above.
The second difficulties
To establish a continue property of the Energy functional $latex E(\Omega)= \frac{Vol(\Omega)}{Surf(\Omega)}$.
the continuous property is consider with all open set $latex \Omega$ with Gromov-Hausdorff metric $latex d(\Omega_1,\Omega_2)= \inf_{metric\ d on \Omega_1 \cup \Omega_2}\sup_{x_1\in \Omega_1, x_2\in \Omega_2}d(x_1,x_2)$.
We need to proof the continuous of $latex E(\Omega)$ with the Gromov-hausdorff metric on the space consist with convex open sets.
To remark,we need to observe that polygon approximation is just corresponding to the $latex \delta-seperate$ points approximation in Gromov-hausdorff distance. and definitely carefully refinement of this kind of approximation could lead to the result of continuous of the energy $latex E(\Omega)$ on convex set.
A second remark, we definitely need a definition of the $latex surf(\Omega)$ it could be achieve with open convex set $latex \Omega$ by a outer and inter approximation by polygon and the error term estimate.
Further remark, isoperimetric inequality is a general phenomenon.