Title: Constructing a Metric by Pullback on a Linear Normalized Space
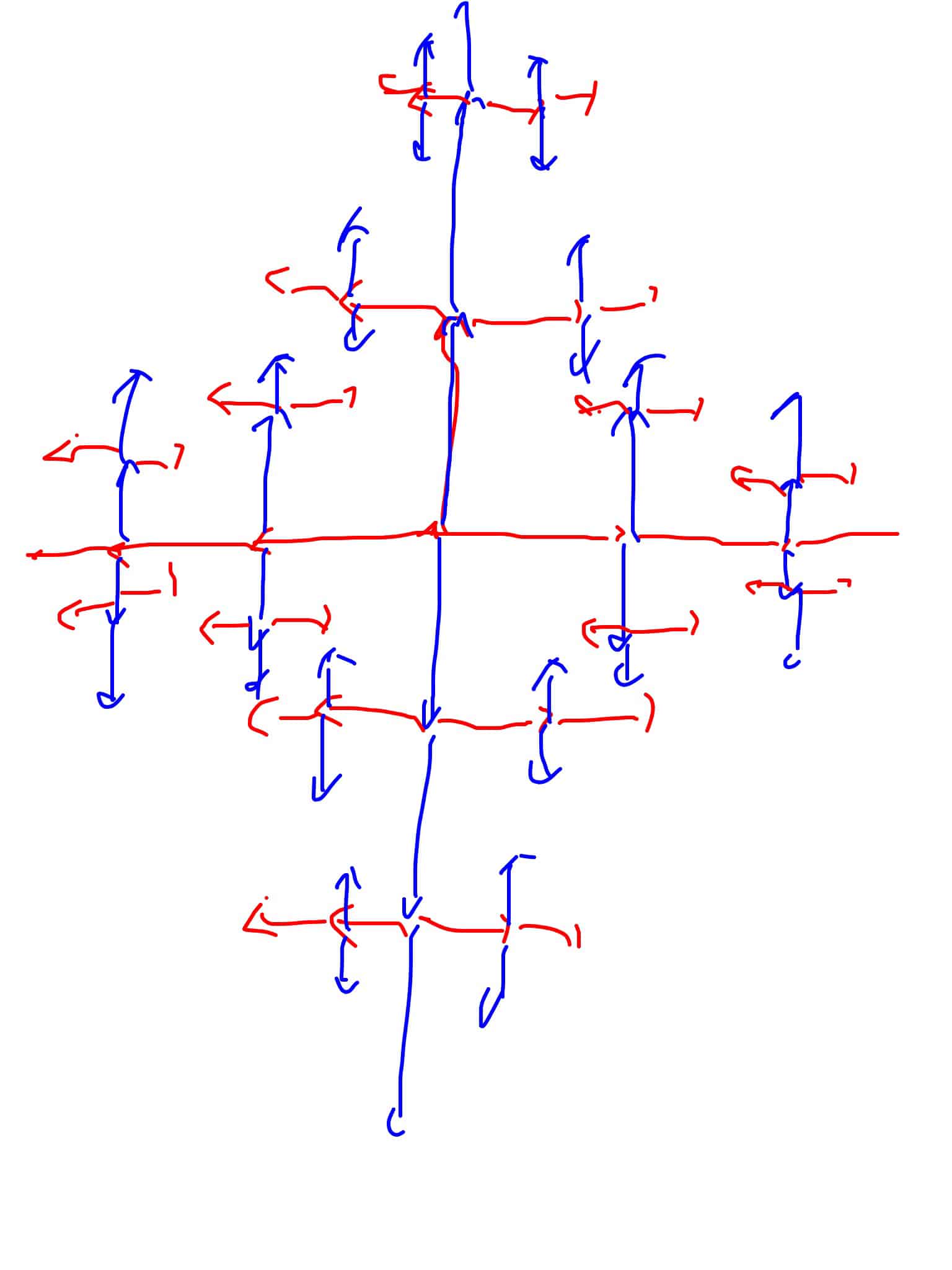
In this article, we aim to construct a metric by pulling back a metric on a suitable linear normalized space $H$ that we carefully constructed. We begin by defining the generators of the free group $F_2$ as $a$ and $b$.
Step 1: Constructing the Linear Normalized Space $H
We construct the linear normalized space $H$, which is spanned by the basis $\Lambda = \Lambda_a \cup \Lambda_b$. Here, $\Lambda_a$ and $\Lambda_b$ are defined by examining the Cayley graph of $F_2$. For every level set of vertical vectors in the Cayley graph, we assign a basis in $\Lambda_a$. Similarly, for horizontal vectors, we assign a basis in $\Lambda_b$. By spanning this with coefficients from $\mathbb{Z}$, we obtain a linear space $V$. By Zorn’s lemma, there exists a norm on the space, denoted as $|\cdot|$. Thus, we have successfully constructed $H = (V, |\cdot|)$.
Step 2: Pulling Back the Norm $|\cdot|$ to $F_2$
We establish a natural bijection $T: F_2 \to H$. This bijection is defined by considering the Cayley graph embedded in $\mathbb{R}^2$, where each element in $F_2$ corresponds to a point in the Cayley graph. By identifying elements in $F_2$ with points in the Cayley graph using the shortest path, we can explain why the path lies in $H$. This path only crosses a finite number of vertical and horizontal levels, and on each level, it only passes a finite number of steps. Thus, we have defined the bijection $T: F_2 \to H$, which allows us to pull back the norm on $H$ to a norm on $F_2.
Step 3: Proof of the Satisfied Conditions
We proceed to prove that the norm obtained by pullback satisfies the required conditions. We only need to prove the conditions of linear growth and the triangle inequality. The conjugation invariance is automatically satisfied by linear growth. The triangle inequality is also automatically satisfied due to the bijection $T$ preserving the structure. However, it is important to note that the multiplier of elements $x_1, x_2 \in F_2$ cannot be viewed as putting the two paths together, as the addition operation is not commutative.
In conclusion, the space we should consider is the path space equipped with the composition operation. It is conceivable that there exists a “big space” such that the natural metric on the “big space” restricts the embedding image of $F_2$ to a linear growth metric.