Consider a compact one-dimensional dynamic system.
We focus on $S_1$, it does not mean $S_1$ is the only compact one-dimensional system, but it is a typical example.
Let $T: S_1 \rightarrow S_1$.
If $T$ is a homomorphism, then $T$ stays the order of $S_1$ (by continuity and the zero point theorem). This just means:
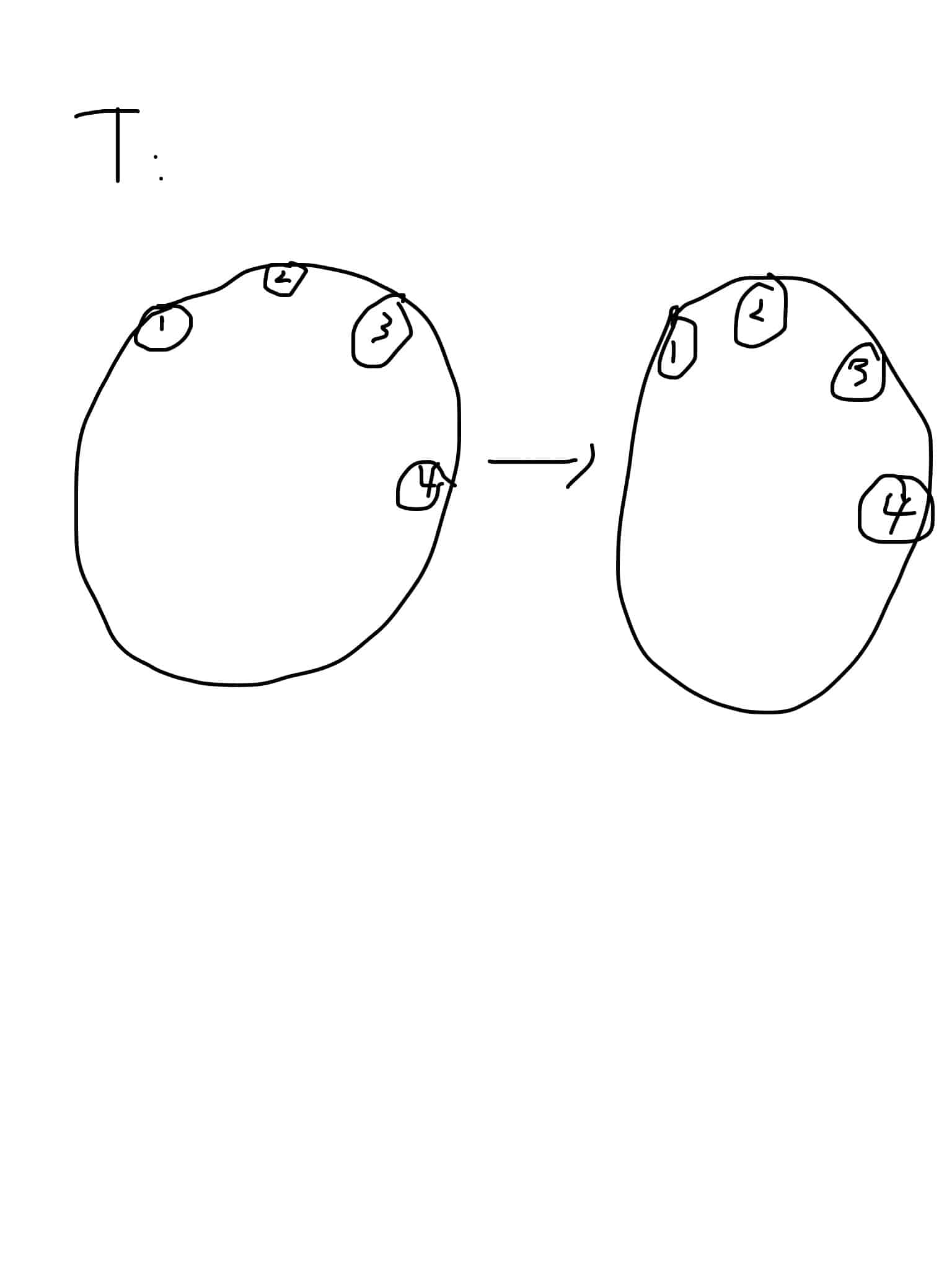
(may be do a reflexion $latex e^{2\pi i\theta}\to e^{-2\pi i\theta}$).
In the homomorphism case, we try to define the rotation number to describe the expanding rate of the dynamic system.
Let $T: \mathbb{S}_1 \to \mathbb{S}_1$, i.e., $T:\mathbb{R}/\mathbb{Z} \to \mathbb{R}/\mathbb{Z}$. Lifting to,
$\hat{T}:\mathbb{R} \to \mathbb{R}$.
How to realize the lifting?
Step 1: Periodic extend $T:\mathbb{S}_1 \to \mathbb{S}_1$ to $T’: \mathbb{R} \to \mathbb{S}_1$. (Regard $\mathbb{S}_1$ as $[0,2\pi]$).
Step 2: Consider the “flow” of $T’:\mathbb{R} \to \mathbb{S}_1$. We get $\hat{T}:\mathbb{R} \to \mathbb{R}$.
The rotation number is defined as:
$\rho (T)=\limsup_{n \to \infty}\frac{\hat{T}^n(x)}{n}$.
Following, we will show it is independent of the choice of $x$ and $\rho (T)=\lim_{n \to \infty}\frac{\hat{T}^n(x)}{n}$, in fact.
It is not difficult to prove the following property:
Property:
- If $T’$ is conjugate (in fact semi-conjugate is enough), then the rotation number of $T’$ equals the rotation number of $T$.
- If $T’$ is conjugate to $T$, then the rotation number of $T’$ equals the rotation number of $T$.
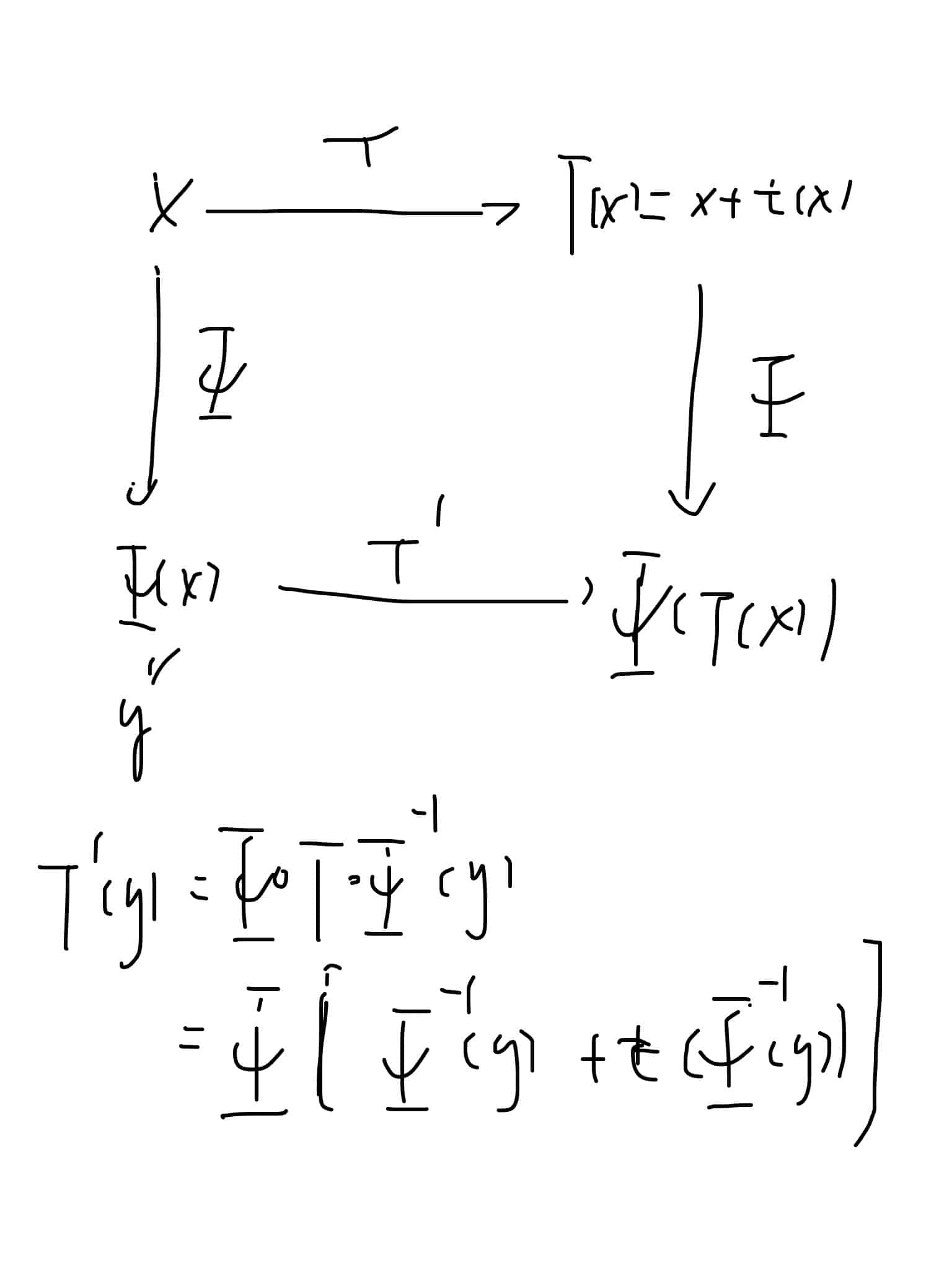
$T'(y)=\Psi\circ T\circ \Psi^{-1}(y)=\Psi(\Psi^{-1}(y)+t(\Psi^{-1}(y)))$)
Example: $T: x\to x+\alpha$, $\alpha\in \mathbb R$. It is not difficult to prove the rotation number of $T$ is $\alpha$.
Proposition:
1) For $n\geq 1$, we have that $\rho(T^n) \equiv \rho(T) \pmod{1}$.
2) If $T$ has a periodic point, i.e. $x\in S_1, \exists n\in \mathbb{N}^*, T^{n}(x)=x$. Then $\rho(T)$ is rational.
3) $T:\mathbb{R}/\mathbb{Z} \to \mathbb{R}/\mathbb{Z}$ has no periodic point, then $\rho(T)$ is irrational.
4) The limit actually exists and we have: $\rho(T)=\lim_{n\to \infty}\frac{\hat T^n(x)}{n} \pmod{1}$.
Proof of 1):
$\rho(T^n)=\lim_{k\to \infty}\frac{(\hat T^n)^{k}(x)}{k}$
$= \lim_{k\to \infty}n\frac{(\hat T)^{nk}(x)}{nk}$
$= n\rho (T)$.
Used the property $|x-y|<k \leftrightarrow |T^{\omega}(x)-T^{\omega}(y)|<k+1, \forall \omega\in \mathbb{N}^*, \forall k\in \mathbb{Z}^{+}$.
Proof of 2):
It is not difficult to prove $\rho(T)$ is independent of the choice of $x$. So choose $x$ to be the periodic point.
Remark: But the inverse of 2) is not true. For example:
$x\mapsto x+\frac{1}{2}+\frac{1}{100}\sin(4\pi x)$.
This dynamic system has both periodic points (${0,\frac{1}{2}},{\frac{1}{4},\frac{3}{4}}$) and non-periodic points (maybe orbits generated by ${\frac{1}{\sqrt{2}}}$).
Proof of 3):
If not, assume $\rho(T)$ is a rational number $\frac{q}{p}$. Take any point $x\in S_1$, then:
$\lim_{n\to \infty}\frac{\hat T^n(x)}{n}=\frac{q}{p}$.
$\Longrightarrow \lim_{n\to \infty}\frac{(\hat T^p)(x)}{n}=q$.
$\Longrightarrow \lim_{n\to \infty}\frac{(\hat T^p-q)^n(x)}{n}=0$.
Now assume $\hat T^p-q=\widetilde T$.
Then $\widetilde x>x$, $\forall x\in S_1$ (if $\widetilde x<x, \forall x\in S_1$, take reflection $x\mapsto -x$).
And there do not exist $n\in \mathbb{N}^*$ such that $\widetilde T^nx>x+1$. If not, we could prove the rotation number is larger than $\frac{1}{n}$ leading to a contradiction.
So ${\widetilde T^nx}_{n=1}^{\infty}$ is a bounded monotonically increasing sequence in $S_1$, its limit point $z\in S_1$ must satisfy $\widetilde T^n (z)=z$.
Proof of 4):
Using the pointwise approximation inequality induced from the monotonically and stay ordering property of $\mathbb{S}_1$ by $T$.
Corollary:
Assume $ho(T)$ is irrational.
- Let $n_1,n_2,m_1,m_2\in \mathbb{Z}$, and $x,y\in \mathbb{R}$. If $\hat{T}^{n_1}(x)+m_1<\hat{T}^{n_2}(x)+m_2$, then $\hat{T}^{n_1}(y)+m_1<\hat{T}^{n_2}(y)+m_2$.
- The bijection $n\ho(T)+m \mapsto \hat{T}^n(0)+m$ between the set $\Omega={n\ho(T)+m| n,m\in \mathbb{Z}}$ and $\Gamma={\hat{T}^{n}(0)+m,n,m\in \mathbb{Z}}$ preserves the natural ordering on $\mathbb{R}$.
This corollary is not difficult to prove using the established property.
Denjoy’s theorem
Proposition:
If $T: \mathbb{R}/\mathbb{Z} \to \mathbb{R}/\mathbb{Z}$ is a minimal orientation-preserving homeomorphism with irrational rotation number $ho$ then $T$ is topologically conjugate to the standard rotation $R_{ho}: \mathbb{R}/\mathbb{Z} \to \mathbb{R}/\mathbb{Z}$.
Proof left as an exercise.
For $T: \mathbb{R}/\mathbb{Z} \to \mathbb{R}/\mathbb{Z}$, $T’: \mathbb{R}/\mathbb{Z} \to \mathbb{R}$. We define the variation of $\log|T’|: \mathbb{R}/\mathbb{Z} \to \mathbb{R}$ by:
$Var(\log(|T’|))=$
$sup{\sum_{i=0}^{n-1}|log|T’|(x_{i+1})-log|T’|(x_i)|: 0=x_0<x_1<…<x_n=1}$
We say that the logarithm of $|T’|$ has bounded variation if this value $Var(\log|T’|) $ is finite.
Denjoy’s theorem:
If $T: \mathbb{R}/\mathbb{Z} \to \mathbb{R}/\mathbb{Z}$ is a $C^1$ orientation-preserving homeomorphism of the circle with derivative of standard variation and irrational rotation number $ho=ho(T)$ then $T:\mathbb{R}/\mathbb{Z} \to \mathbb{R}/\mathbb{Z}$ is topologically conjugate to the standard rotation :
$R_{ho}:\mathbb{R}/\mathbb{Z} \to \mathbb{R}/\mathbb{Z$.
Due to the upper proposition, we only need to show $T:\mathbb{R}/\mathbb{Z} \to \mathbb{R}/\mathbb{Z}$ is minimal. Proof of minimal is split into the following two sub-lemmas.
Sub-lemma 1:
If $T$ has an irrational rotation number and there are a constant $C>0$ and a sequence of integers $q_n \to \infty$ such that the map: $T: \mathbb{R}/\mathbb{Z} \to \mathbb{R}/\mathbb{Z}$ satisfies: $|(T^{q_n})'(x)||(T^{-q_n})'(x)|\geq C$ Then $T: \mathbb{R}/\mathbb{Z} \to \mathbb{R}/\mathbb{Z}$ is minimal.
Sub-lemma 2:
Fix $x\in \mathbb{R}/\mathbb{Z}$ and write $x_n=T^n(x)$, for $x\in \mathbb{Z}$. There exists an increasing sequence $q_n \to \infty$ of natural numbers such that the intervals $(x_0,x_{q_n}),(x_1,x_{q_n+1}),…,(x_i,x_{q_n+i}),…,(x_{q_n},x_{2q_n})$ are all disjoint.
Paradox and problem
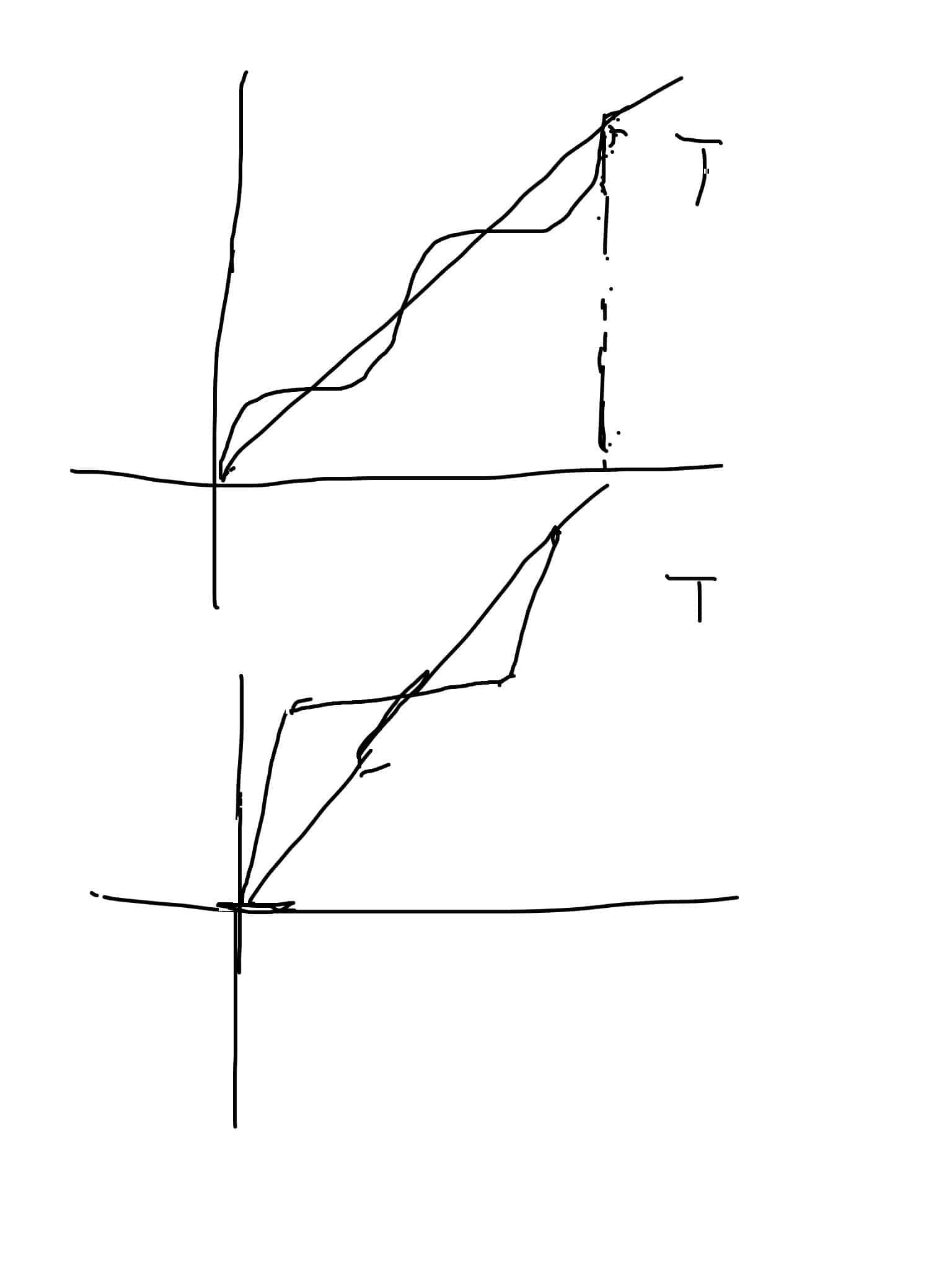
Graph:
$\rho(T)>0$ because of existence of fix point.
$T_{\alpha}=T+\alpha$ for $latex \alpha< sup_x|T_x-x|$.
Is $\rho(T_{\alpha})=0$ always true for $latex \alpha \in R$?
If it is right, then there is a contradiction with argument $ (*)$, but for what type of dynamic system $latex T$?
$T_{\alpha}=T+\alpha$ satisfied $\rho(T_{\alpha})=\rho(T)+\alpha$. for all $latex \alpha\in \mathbb R$?
Problem:
If $T $ is not homomorphism but $T:x\to x+g(x)$ induced $g(x)=x-f(x)$, $f(x)$ is striating increasing, Is the limit of $ \lim_{x\to \infty}\frac{\hat T(x)}{n}$ always exists? it could not be increase with $latex x$.